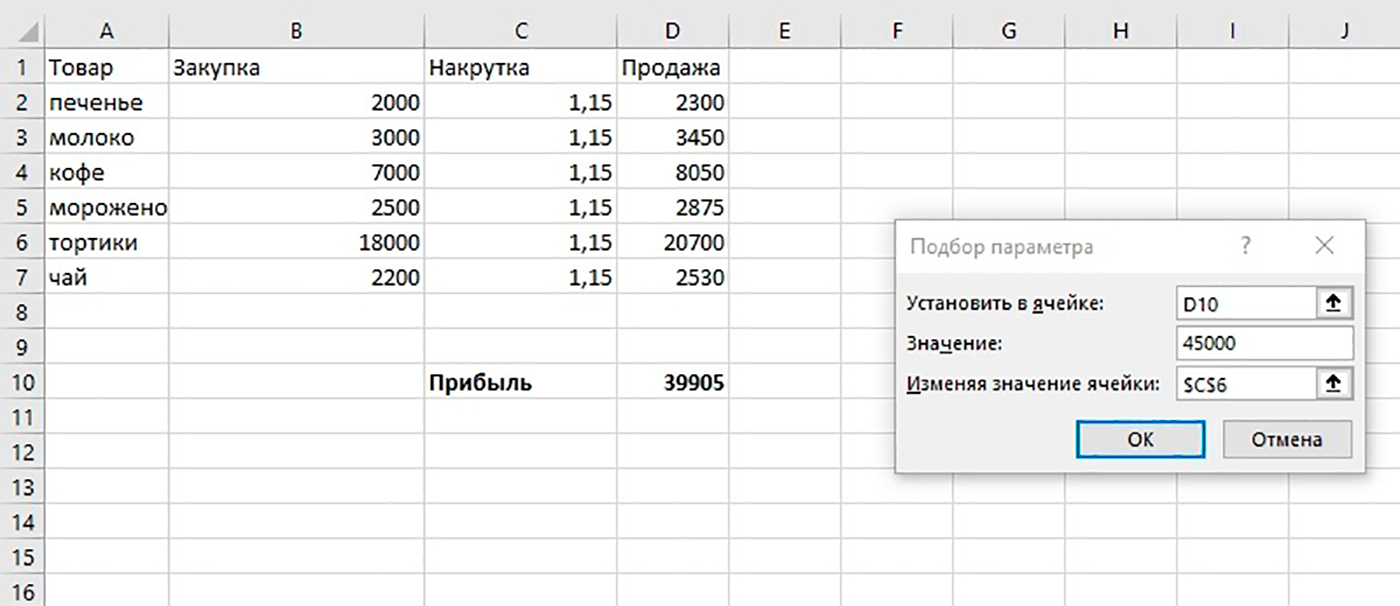
Коэффициент корреляции в excel

Сфера использования понятия

Корреляция широко распространена в разных видах деятельности с целью обработки массивов статистических данных. Это касается, прежде всего, таких наук, как:

• экономика;
• математика;
• астрофизика;
• психология;
• социология и др.

Отдельно стоит выделить возможность применения корреляции в некоторых важных для человечества сферах деятельности. Это касается металловедения, агрохимии, биометрического анализа и биологии. В разных типах прикладных отраслей принято использовать предельные границы интервалов для оценки тесноты или же значимости связи.

Распространение использования метода корреляции обусловлено такими факторами, как:

• простота подсчета;
• отсутствие необходимости наличия специальной подготовки.

Интерпретация корреляции тоже под силы практически любому человеку. Именно поэтому данный метод так широко используется в различных сферах, где требуется анализ тех или иных статистических данных.

Примеры решений онлайн: линейная регрессия

Простая выборка

Пример 1. Имеются данные средней выработки на одного рабочего Y (тыс. руб.) и товарооборота X (тыс. руб.) в 20 магазинах за квартал. На основе указанных данных требуется:
1) определить зависимость (коэффициент корреляции) средней выработки на одного рабочего от товарооборота,
2) составить уравнение прямой регрессии этой зависимости.

Пример 2. С целью анализа взаимного влияния зарплаты и текучести рабочей силы на пяти однотипных фирмах с одинаковым числом работников проведены измерения уровня месячной зарплаты Х и числа уволившихся за год рабочих Y:
X 100 150 200 250 300
Y 60 35 20 20 15
Найти линейную регрессию Y на X, выборочный коэффициент корреляции.

Пример 3. Найти выборочные числовые характеристики и выборочное уравнение линейной регрессии $y_x=ax+b$. Построить прямую регрессии и изобразить на плоскости точки $(x,y)$ из таблицы. Вычислить остаточную дисперсию. Проверить адекватность линейной регрессионной модели по коэффициенту детерминации.

Пример 4. Вычислить коэффициенты уравнения регрессии. Определить выборочный коэффициент корреляции между плотностью древесины маньчжурского ясеня и его прочностью. Решая задачу необходимо построить поле корреляции, по виду поля определить вид зависимости, написать общий вид уравнения регрессии Y на Х, определить коэффициенты уравнения регрессии и вычислить коэффициенты корреляции между двумя заданными величинами.

Пример 5. Компанию по прокату автомобилей интересует зависимость между пробегом автомобилей X и стоимостью ежемесячного технического обслуживания Y. Для выяснения характера этой связи было отобрано 15 автомобилей. Постройте график исходных данных и определите по нему характер зависимости. Рассчитайте выборочный коэффициент линейной корреляции Пирсона, проверьте его значимость при 0,05. Постройте уравнение регрессии и дайте интерпретацию полученных результатов.

Корреляционная таблица

Пример 6. Найти выборочное уравнение прямой регрессии Y на X по заданной корреляционной таблице

Пример 7. В таблице 2 приведены данные зависимости потребления Y (усл. ед.) от дохода X (усл. ед.) для некоторых домашних хозяйств.
1. В предположении, что между X и Y существует линейная зависимость, найдите точечные оценки коэффициентов линейной регрессии.
2. Найдите стандартное отклонение $s$ и коэффициент детерминации $R^2$.
3. В предположении нормальности случайной составляющей регрессионной модели проверьте гипотезу об отсутствии линейной зависимости между Y и X.
4. Каково ожидаемое потребление домашнего хозяйства с доходом $x_n=7$ усл. ед.? Найдите доверительный интервал для прогноза.
Дайте интерпретацию полученных результатов. Уровень значимости во всех случаях считать равным 0,05.

Решение об исследовании зависимости (4 страницы)

Пример 8. Распределение 100 новых видов тарифов на сотовую связь всех известных мобильных систем X (ден. ед.) и выручка от них Y (ден.ед.) приводится в таблице:
Необходимо:
1) Вычислить групповые средние и построить эмпирические линии регрессии;
2) Предполагая, что между переменными X и Y существует линейная корреляционная зависимость:
А) найти уравнения прямых регрессии, построить их графики на одном чертеже с эмпирическими линиями регрессии и дать экономическую интерпретацию полученных уравнений;
Б) вычислить коэффициент корреляции, на уровне значимости 0,05 оценить его значимость и сделать вывод о тесноте и направлении связи между переменными X и Y;
В) используя соответствующее уравнение регрессии, оценить среднюю выручку от мобильных систем с 20 новыми видами тарифов.

Коэффициент корреляции

Пример 9. На основании 18 наблюдений установлено, что на 64% вес X кондитерских изделий зависит от их объема Y. Можно ли на уровне значимости 0,05 утверждать, что между X и Y существует зависимость?

Пример 10. Исследование 27 семей по среднедушевому доходу (Х) и сбережениям (Y) дало результаты: $\overline{X}=82$ у.е., $S_x=31$ у.е., $\overline{Y}=39$ у.е., $S_y=29$ у.е., $\overline{XY} =3709$ (у.е.)2. При $\alpha=0,05$ проверить наличие линейной связи между Х и Y. Определить размер сбережений семей, имеющих среднедушевой доход $Х=130$ у.е.

Нужно решить задачи по на тему регрессия и корреляция?

Оставьте заявку сегодня

Дополнительное замечание про распределения:

нормально ли, что анализируя данные геофизического мониторинга, мы никогда не встречаемся с нормальным распределением? 

Да-да, я в курсе про Центральную предельную теорему. Но еще больше я склонен верить практике обработки тысяч различных экспериментальных сигналов — прежде всего, данных геофизического мониторинга, но далеко не только его. Поэтому большая просьба к тем «чистым» математикам, которых задевает утверждение, что отсутствие нормальности — это нормально: не надо ругаться! Просто возьмите десяток-другой экспериментальных рядов, полученных в результате длительных (многие недели и месяцы) наблюдений и содержащих достаточное количество точек данных (десятки тысяч и более). И попробуйте найти среди них такие, чье распределение неотличимо от нормального, например, по критерию хи-квадрат. К сожалению или к счастью, жизнь несколько отличается от

Можно с уверенностью утверждать, что для подавляющего большинства сигналов, получаемых при долговременном мониторинге, условия ЦПТ не выполнены. Во-первых, нет никаких гарантий, что поведение контролируемой величины зависит от многих малых и независимых причинных факторов — наоборот, обычно они коррелированы между собой, а вклад некоторых преобладает

Но еще более важно, что практически все природные процессы нестационарны, что сразу же выводит их за рамки явлений, к которым может быть применена ЦПТ. Впрочем, это уже отдельный вопрос, который обсуждается в

Функция КОРРЕЛ для определения взаимосвязи и корреляции в Excel

КОРРЕЛ – функция, применяемая для подсчета коэффициента корреляции между 2-мя массивами. Разберем на четырех примерах все способности этой функции.

Примеры использования функции КОРРЕЛ в Excel

Первый пример. Есть табличка, в которой расписана информация об усредненных показателях заработной платы работников компании на протяжении одиннадцати лет и курсе $. Необходимо выявить связь между этими 2-умя величинами. Табличка выглядит следующим образом:

24

Алгоритм расчёта выглядит следующим образом:

25

Отображенный показатель близок к 1. Результат:

26

Определение коэффициента корреляции влияния действий на результат

Второй пример. Два претендента обратились за помощью к двум разным агентствам для реализации рекламного продвижения длительностью в пятнадцать суток. Каждые сутки проводился социальный опрос, определяющий степень поддержки каждого претендента. Любой опрошенный мог выбрать одного из двух претендентов или же выступить против всех. Необходимо определить, как сильно повлияло каждое рекламное продвижение на степень поддержки претендентов, какая компания эффективней.

27

Используя нижеприведенные формулы, рассчитаем коэффициент корреляции:

• =КОРРЕЛ(А3:А17;В3:В17).
• =КОРРЕЛ(А3:А17;С3:С17).

Результаты:

28

Из полученных результатов становится понятно, что степень поддержки 1-го претендента повышалась с каждыми сутками проведения рекламного продвижения, следовательно, коэффициент корреляции приближается к 1. При запуске рекламы другой претендент обладал большим числом доверия, и на протяжении 5 дней была положительная динамика. Потом степень доверия понизилась и к пятнадцатым суткам опустилась ниже изначальных показателей. Низкие показатели говорят о том, что рекламное продвижение отрицательно повлияло на поддержку. Не стоит забывать, что на показатели могли повлиять и остальные сопутствующие факторы, не рассматриваемые в табличной форме.

Анализ популярности контента по корреляции просмотров и репостов видео

Третий пример. Человек для продвижения собственных роликов на видеохостинге Ютуб применяет соцсети для рекламирования канала. Он замечает, что существует некая взаимосвязь между числом репостов в соцсетях и количеством просмотров на канале. Можно ли про помощи инструментов табличного процессора произвести прогноз будущих показателей? Необходимо выявить резонность применения уравнения линейной регрессии для прогнозирования числа просмотров видеозаписей в зависимости от количества репостов. Табличка со значениями:

29

Теперь необходимо провести определение наличия связи между 2-мя показателями по нижеприведенной формуле:

0,7;ЕСЛИ(КОРРЕЛ(A3:A8;B3:B8)>0,7;”Сильная  прямая зависимость”;”Сильная обратная зависимость”);”Слабая зависимость или ее отсутствие”)’ class=’formula’>

Если полученный коэффициент выше 0,7, то целесообразней применять функцию линейной регрессии. В рассматриваемом примере делаем:

30

Теперь производим построение графика:

31

Применяем это уравнение, чтобы определить число просматриваний при 200, 500 и 1000 репостов: =9,2937*D4-206,12. Получаем следующие результаты:

32

Функция ПРЕДСКАЗ позволяет определить число просмотров в моменте, если было проведено, к примеру, двести пятьдесят репостов. Применяем: 0,7;ПРЕДСКАЗ(D7;B3:B8;A3:A8);”Величины не взаимосвязаны”)’ class=’formula’>. Получаем следующие результаты:

33

Особенности использования функции КОРРЕЛ в Excel

Данная функция имеет нижеприведенные особенности:

1. Не учитываются ячейки пустого типа.
2. Не учитываются ячейки, в которых находится информация типа Boolean и Text.
3. Двойное отрицание «–» применяется для учёта логических величин в виде чисел.
4. Количество ячеек в исследуемых массивах обязаны совпадать, иначе будет выведено сообщение #Н/Д.

Коэффициент корреляции

Рисунок 4. Сравнение автокорреляционной функции (АКФ) и кросскорреляционной функции (ВКФ) для трех разных отведений

Значение корреляционного анализа состоит в нахождении автокорреляционной функции, которая показывает преобладающие ритмы, или взаимно-корреляционной функции, отражающей связь фрагмента обрабатываемого сигнала и эталона сигнала без помех и шумов или же связь между двумя неочищенными сигналами. (рис. 4) Биомедицинские сигналы относятся к квазипериодическим сигналам. ЭЭГ-сигналы содержат эпохи, имеющие схожие друг с другом характеристики. Эпоха ЭЭГ-сигнала – это произвольно выделенный период времени в записи ЭЭГ (чаще всего составляет 10 с.) В качестве эталона какой-либо эпохи ЭЭГ-сигнала используется либо стандартный фрагмент данного сигнала, свободный от помех и шумов, либо искусственно созданная модель стандартного фрагмента ЭЭГ-сигнала, построенная на основе заранее известных данных о форме и амплитудно-временных характеристик “чистого” фрагмента. Сравнение автокорреляционной функции (АКФ) и кросскорреляционной функции (ВКФ) для трех разных отведений представлено на рис. 4.  График под буквой г изображает автокорреляционную функцию фрагмента а. Подобная функция графика свидетельствует о том, что сходство двух эпох данного сигнала сходит на ноль относительно медленно. Следовательно, мы можем сделать вывод о периодичности процессов, протекающих в данном отведении, т.к. отдельные его фрагменты достаточно сильно схожи друг с другом. Аналогичные выводы можно сделать и о сигнале на графике б, опираясь на его функцию, обозначенную буквой д.

Рисунок 5. Применение корреляционного анализа к обработке ЭЭГ-сигнала

С другой стороны, график в, автокорреляционная функция которого изображена на рисунке е, изображает хаотический процесс, отдельные фрагменты которого не подобны друг другу. Об этом свидетельствует крайне быстрое затухание его автокорреляционной функции. Т.о. процессы, протекающие в данном отведении, непериодичны, т.к. отдельные фрагменты графика мало схожи друг с другом.

График ж изображает кросс-корреляционную функцию между сигналами а и б. Ее медленное затухание свидетельствует о наличии взаимовлияния фрагментов а и б. График з и график и отражают кросс-корреляционную функцию между сигналами б–в и а–в соответственно. Поскольку затухание графика происходит достаточно быстро, мы можем сделать вывод о том, что между данными отрезками ЭЭГ-сигнала отсутствует существенная взаимосвязь. 

Рисунок 6. Результат сравнения графиков напряжения при использовании сухих и влажных электродов

Корреляционный анализ применительно к исправлению графика ЭЭГ можно изобразить так: в центре иллюстрации приведено два графика – график воздействия стимула сверху (синий цвет) и фрагмент ЭЭГ снизу (синий цвет).  (рис. 5)

В правой части иллюстрации изображены графики скорости воздействия стимула (синий цвет) и средней формы волны (розовый цвет). Последний был получен путем суммации изначальных ЭЭГ-графиков. Их также подвергли кросскорелляционному анализу, результат которого приведен ниже (розовый цвет). Затем, используя полученные данные о корреляции, был построен исправленный график ЭЭГ-сигнала (розовый цвет).

В левой части изображены графики скорости воздействия стимула (синий цвет) и мощности ЭЭГ (зеленый цвет). Их подвергли кросскорелляционному анализу, результат которого приведен ниже (зеленый цвет). Затем, используя полученные данные о корреляции, был построен исправленный график ЭЭГ-сигнала (зеленый цвет).

В случае, изображенном на рис. 6, сравниваются графики напряжения при использовании сухих (красный) и влажных (синий) электродов. Степень корреляции результатов представлена в виде графика черного цвета в верхней части изображения.

Использование MS EXCEL для расчета ковариации

Ковариация

близка по смыслу с (также является мерой разброса) с тем отличием, что она определена для 2-х переменных, адисперсия — для одной. Поэтому, cov(x;x)=VAR(x).

Для вычисления ковариации в MS EXCEL (начиная с версии 2010 года) используются функции КОВАРИАЦИЯ.Г() и КОВАРИАЦИЯ.В() . В первом случае формула для вычисления аналогична вышеуказанной (окончание .Г

обозначаетГенеральная совокупность ), во втором – вместо множителя 1/n используется 1/(n-1), т.е. окончание.В обозначаетВыборка .

Примечание

: Функция КОВАР() , которая присутствует в MS EXCEL более ранних версий, аналогична функции КОВАРИАЦИЯ.Г() .

Примечание

: Функции КОРРЕЛ() и КОВАР() в английской версии представлены как CORREL и COVAR. Функции КОВАРИАЦИЯ.Г() и КОВАРИАЦИЯ.В() как COVARIANCE.P и COVARIANCE.S.

Дополнительные формулы для расчета ковариации

=СУММПРОИЗВ(B28:B88-СРЗНАЧ(B28:B88);(D28:D88-СРЗНАЧ(D28:D88)))/СЧЁТ(D28:D88)

=СУММПРОИЗВ(B28:B88-СРЗНАЧ(B28:B88);(D28:D88))/СЧЁТ(D28:D88)

=СУММПРОИЗВ(B28:B88;D28:D88)/СЧЁТ(D28:D88)-СРЗНАЧ(B28:B88)*СРЗНАЧ(D28:D88)

Эти формулы используют свойство ковариации

Если переменные x

иy независимые, то их ковариация равна 0. Если переменные не являются независимыми, то дисперсия их суммы равна:

VAR(x+y)= VAR(x)+ VAR(y)+2COV(x;y)

А дисперсия

их разности равна

VAR(x-y)= VAR(x)+ VAR(y)-2COV(x;y)

Ковариантность прекрасна, но …

Ковариантность — это прекрасный способ количественно оценить движение переменных относительно друг друга, но у него есть некоторые проблемы.

Отличающиеся единицы:Ковариацию трудно интерпретировать, когда единицы двух переменных различны. Например, еслиИксв долларах иYнаходится в фунтах стерлингов единица ковариации междуИкса такжеYстановитсядолларовые времена фунт стерлингов, Как можно это интерпретировать? Даже когда обаИкса такжеYимеют одну и ту же единицу, скажем, доллар, единицы ковариации становится …доллар раз доллар!Все еще не легко понять. Облом!

Отличающиеся весы:Существует также проблема дальности. когдаИкса такжеYварьируются в течение небольшого интервала, скажемвы получите обманчиво крошечное значение ковариации, даже еслиИкса такжеYдвигаться вместе очень плотно.

Сложность со сравнением:Потому чтоИкса такжеYмогут иметь разные единицы измерения и разные диапазоны, зачастую невозможно объективно сравнить ковариацию между одной парой переменных и другой парой переменных. Скажи я хочу сравнитьнасколько сильнее или слабееэто линейная зависимость междуэкономия топлива и длина автомобиляпо сравнению с отношением междуэкономия топлива и снаряженная масса, Использование ковариации для этого сравнения потребует сравнения двух значений в двух разных единицах и двух разных диапазонах. Проблематично, если не сказать больше.

Если бы мы только могли масштабировать ковариацию, чтобы диапазон был стандартизирован, а также решить проблему «единиц» Введите «стандартное отклонение». Проще говоря, стандартное отклонение измеряет среднее отклонение данных от их среднего значения. Стандартное отклонение также имеет приятное свойство: он имеет ту же единицу, что и исходная переменная. Итак, давайте разделим ковариацию на стандартные отклонения двух переменных. Это приведет к изменению масштаба ковариации, так что теперь она выражается вкратные стандартному отклонениюи это будет такжеотмените единицы измерения из числителя, Все неприятности с ковариацией решаются в двух простых делениях! Вот полученная формула:

Где же мы видели эту формулу раньше? Это, конечно, коэффициент корреляции Пирсона!

Как выполняется корреляция в Excel?

«Корреляция» в переводе с латинского обозначает «соотношение», «взаимосвязь». Количественная характеристика взаимосвязи может быть получена при вычислении коэффициента корреляции.

Этот популярный в статистических анализах коэффициент показывает, связаны ли какие-либо параметры друг с другом (например, рост и вес; уровень интеллекта и успеваемость; количество травм и продолжительность работы).

Использование корреляции

Вычисление корреляции особенно широко используется в экономике, социологических исследованиях, медицине и биометрии — везде, где можно получить два массива данных, между которыми может обнаружиться связь.

Рассчитать корреляцию можно вручную, выполняя несложные арифметические действия. Однако процесс вычисления оказывается очень трудоемким, если набор данных велик. Особенность метода в том, что он требует сбора большого количества исходных данных, чтобы наиболее точно отобразить, есть ли связь между признаками.

Поэтому серьезное использование корреляционного анализа невозможно без применения вычислительной техники. Одной из наиболее популярных и доступных программ для решения этой задачи является Microsoft Office Excel.

Как выполнить корреляцию в Excel?

Самым трудоемким этапом определения корреляции является набор массива данных. Сравниваемые данные располагаются обычно в двух колонках или строчках. Таблицу следует делать без пропусков в ячейках. Современные версии Excel (с 2007 и младше) не требуют установок дополнительных настроек для статистических расчетов; необходимые манипуляции можно сделать в разделе формул:

1. Выбрать пустую ячейку, в которую будет выведен результат расчетов.
2. Нажать в главном меню Excel пункт «Формулы».
3. Среди кнопок, сгруппированных в «Библиотеку функций», выбрать «Другие функции».
4. В выпадающих списках выбрать функцию расчета корреляции (Статистические — КОРРЕЛ).
5. В Excel откроется панель «Аргументы функции». «Массив 1» и «Массив 2» — это диапазоны сравниваемых данных. Для автоматического заполнения этих полей можно просто выделить нужные ячейки таблицы.
6. Нажать «ОК», закрыв окно аргументов функции. В ячейке появится подсчитанный коэффициент корреляции.

Корреляция может быть прямая (если коэффициент больше нуля) и обратная (от -1 до 0).

Первая означает, что при росте одного параметра растет и другой. Обратная (отрицательная) корреляция отражает факт, что при росте одной переменной другая уменьшается.

Корреляция может быть близка к нулю. Это обычно свидетельствует, что исследуемые параметры не связаны друг с другом. Но иногда нулевая корреляция возникает, если сделана неудачная выборка, которая не отразила связь, либо связь имеет сложный нелинейный характер.

Если коэффициент показывает среднюю или сильную взаимосвязь (от ±0,5 до ±0,99), следует помнить, что это лишь статистическая взаимосвязь, которая вовсе не гарантирует влияние одного параметра на другой. Также нельзя исключать ситуации, что оба параметра независимы друг от друга, но на них воздействует какой-нибудь третий неучтенный фактор.

Excel помогает моментально вычислить коэффициент корреляции, но обычно только количественных методов недостаточно для установления причинно-следственных связей в соотносимых выборках.

Особенности корреляционного анализа

Под корреляционным анализом подразумевает методика обработки данных статистики. Для этого определяется теснота связи между несколькими переменными, которые необходимо исследовать.

Нередко корреляционный анализ проводят совместно с регрессионным. В таком случае удается получить более развернутые данные, уменьшив при этом влияние на конечный результат тех или иных посторонних факторов.

Основные ограничения корреляционного анализа заключаются в следующем:

1. Применяться эта методика может только в тех случаях, когда присутствует достаточный объем наблюдений для исследования. Он должно быть довольно значительным – в 5 или 6 раз выше, чем количество внешних факторов.
2. Весь объем имеющихся значений и результатов обязательно должен быть подвержен многомерному нормальному распределению. Без этого получить корректный результат исследования просто невозможно.
3. Исходный объем всех полученных значений первоначально должен быть предельно однородным.
4. Результат корреляционного анализа не позволяет сделать вывод о том, какая из переменных была триггером изменений в системе.

Несмотря на вышеперечисленные ограничения, свойственные корреляционному анализу, он пользуется значительной популярностью.

Критерии и методы

КРИТЕРИЙ СПИРМЕНА

Коэффициент ранговой корреляции Спирмена – это непараметрический метод, который используется с целью статистического изучения связи между явлениями. В этом случае определяется фактическая степень параллелизма между двумя количественными рядами изучаемых признаков и дается оценка тесноты установленной связи с помощью количественно выраженного коэффициента.

Чарльз Эдвард Спирмен

1. История разработки коэффициента ранговой корреляции

Данный критерий был разработан и предложен для проведения корреляционного анализа в 1904 году Чарльзом Эдвардом Спирменом, английским психологом, профессором Лондонского и Честерфилдского университетов.

2. Для чего используется коэффициент Спирмена?

Коэффициент ранговой корреляции Спирмена используется для выявления и оценки тесноты связи между двумя рядами сопоставляемых количественных показателей. В том случае, если ранги показателей, упорядоченных по степени возрастания или убывания, в большинстве случаев совпадают (большему значению одного показателя соответствует большее значение другого показателя — например, при сопоставлении роста пациента и его массы тела), делается вывод о наличии прямой корреляционной связи. Если ранги показателей имеют противоположную направленность (большему значению одного показателя соответствует меньшее значение другого — например, при сопоставлении возраста и частоты сердечных сокращений), то говорят об обратной связи между показателями.

1. Коэффициент корреляции Спирмена обладает следующими свойствами:
2. Коэффициент корреляции может принимать значения от минус единицы до единицы, причем при rs=1 имеет место строго прямая связь, а при rs= -1 – строго обратная связь.
3. Если коэффициент корреляции отрицательный, то имеет место обратная связь, если положительный, то – прямая связь.
4. Если коэффициент корреляции равен нулю, то связь между величинами практически отсутствует.
5. Чем ближе модуль коэффициента корреляции к единице, тем более сильной является связь между измеряемыми величинами.

3. В каких случаях можно использовать коэффициент Спирмена?

В связи с тем, что коэффициент является методом непараметрического анализа, проверка на нормальность распределения не требуется.

Сопоставляемые показатели могут быть измерены как в непрерывной шкале (например, число эритроцитов в 1 мкл крови), так и в порядковой (например, баллы экспертной оценки от 1 до 5).

Эффективность и качество оценки методом Спирмена снижается, если разница между различными значениями какой-либо из измеряемых величин достаточно велика. Не рекомендуется использовать коэффициент Спирмена, если имеет место неравномерное распределение значений измеряемой величины.

4. Как рассчитать коэффициент Спирмена?

Расчет коэффициента ранговой корреляции Спирмена включает следующие этапы:

1. Сопоставить каждому из признаков их порядковый номер (ранг) по возрастанию или убыванию.
2. Определить разности рангов каждой пары сопоставляемых значений (d).
3. Возвести в квадрат каждую разность и суммировать полученные результаты.
4. Вычислить коэффициент корреляции рангов по формуле:

Определить статистическую значимость коэффициента при помощи t-критерия, рассчитанного по следующей формуле:

5. Как интерпретировать значение коэффициента Спирмена?

При использовании коэффициента ранговой корреляции условно оценивают тесноту связи между признаками, считая значения коэффициента меньше 0,3 — признаком слабой тесноты связи; значения более 0,3, но менее 0,7 — признаком умеренной тесноты связи, а значения 0,7 и более — признаком высокой тесноты связи.

Также для оценки тесноты связи может использоваться шкала Чеддока:

_xy
Теснота (сила) корреляционной связи
менее 0.3
слабая
от 0.3 до 0.5
умеренная
от 0.5 до 0.7
заметная
от 0.7 до 0.9
высокая
более 0.9
весьма высокая

Статистическая значимость полученного коэффициента оценивается при помощи t-критерия Стьюдента. Если расчитанное значение t-критерия меньше табличного при заданном числе степеней свободы, статистическая значимость наблюдаемой взаимосвязи — отсутствует. Если больше, то корреляционная связь считается статистически значимой.