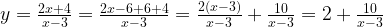Как построить график функции с помощью геометрических преобразований графиков?

Пошаговая инструкция построения графика функции в Excel 2007

1. Запускаем программу, которая создаст новый чистый лист книги Excel. Подписываем два столбца (B и С), в одном из которых будет записан аргумент x, а в другом — функция y.
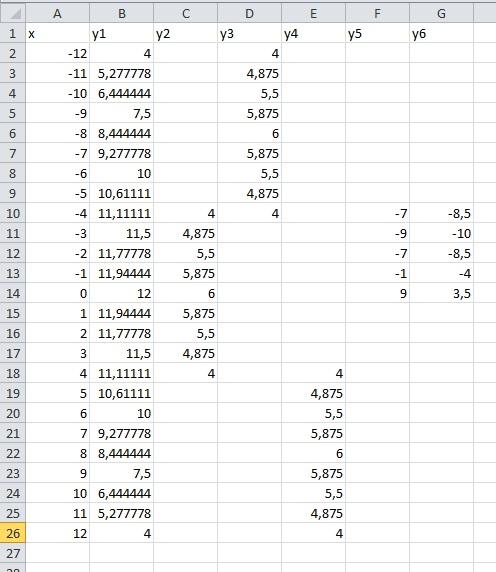
2. Заносим в столбец B, значения аргументов x, начиная с ячейки B3. Можно воспользоваться автоматическим копированием ячеек, предварительно задав шаг (разница между ближайшими значениями аргумента). Значения аргумента x можно задать произвольно, но чаще вводят значения близкие к нулю с учетом отрицательных и положительных значений. Очень хорошо будет смотреться график, если значения будут браться симметрично относительно нуля. Предлагаем выбрать значения в промежутке от -3 до +3 с шагом 0,1. В итоге вы получите 60 значений, по которым график функции будет проложен весьма плавно.
3. Далее, в ячейку C3 забьём формулу функции синуса или ту, которую вам надо построить. Если помните тригонометрию, то функция синуса записывается в виде y = sin x.
4. Однако формулы в Excel отличаются от записей математических формул, и всегда начинаются со знака равно — «=». В нашем примере, вы должны записать в ячейке C3 формулу вида = SIN(B3).
5. Забивать формулу в каждой новой строке очень долго и неудобно (представляете, нужно вбить 60 раз!). Для того чтобы формула была в каждой ячейке необходимо «протянуть» формулу из первой ячейки на все остальные. При этом ссылка на ячейку, откуда берётся значение аргумента будет смещаться построчно.
6. Для этого щёлкаем на ячейке с набранной формулой. В правом нижнем углу ячейки должен появиться небольшой квадратик. Следует навести на него курсор мышки, и когда квадратик превратится в крестик, нажимаем правую кнопку и копируем «протягиванием» формулу вниз на нужное количество ячеек.
7. Переходим к построению графика функции. Заходим в Меню «Вставка» -> «Диаграмма» и выбираем подходящую точечную диаграмму. Жмем волшебную кнопку .
8. В открывшемся окне щелкаем вкладку «Ряд». Добавляем ряд нажатием кнопки .
9. В этом окне нужно задать, из какого диапазона будут выбраны числа для графика. Чтобы выбрать нужные ячейки, следует щёлкнуть поочередно по кнопкам.
10. После этого выделим те ячейки, откуда будут выбраны значения для x и y.
11. Последним шагом станет нажатие кнопки .

Определение 3: Дифференциальное уравнение

Мы описали поведение синуса определенными уравнениями. Вкратце это будет выглядеть так:

Эта красота означает следующее:

Наша текущая позиция — y

Наше ускорение (2-я производная, или у”) — обратно нашей текущей позиции (-y)

Это справедливо и для синуса, и для косинуса. Сначала я просто ненавидел это определение; оно такое непохожее на нашу визуализацию. Я не понимал, что оно описывало суть синуса: «ускорение, обратное текущей позиции».

И вспомните как синус и е связаны? Ну, e^x можно описать уравнением:

То же уравнение с положительным знаком («ускорение равно текущей позиции»)! Когда синус — это «высота окружности», очень тяжело проследить связь с е.

Одним из моих серьезнейших математических сожалений является то, что я еще не изучил дифференциальные уравнения. Но я хочу это сделать, и подозреваю, что правильное понимание синуса и экспоненты сыграют в этом решающую роль.

Примеры использования функций SIN, SINH, COS и COSH в Excel

Пример 1. Путешественник движется вверх на гору с уклоном в 17°. Скорость движения постоянная и составляет 4 км/ч. Определить, на какой высоте относительно начальной точке отсчета он окажется спустя 3 часа.

Таблица данных:

Для решения используем формулу:

=B2*B3*SIN(РАДИАНЫ(B1))

Описание аргументов:

• B2*B3 – произведение скорости на время пути, результатом которого является пройденное расстояние (гипотенуза прямоугольного треугольника);
• SIN(РАДИАНЫ(B1)) – синус угла уклона, выраженного в радианах с помощью функции РАДИАНЫ.

В результате расчетов мы получили величину малого катета прямоугольного треугольника, который характеризует высоту подъема путешественника.

π без картинок

Представьте себе слепого пришельца, который может различать только тени света и темноты. Можете ли вы объяснить ему, что такое π? Довольно сложно пояснить в такой ситуации понятие длины окружности, верно?

Давайте вернемся немного назад. Синус — это циклическая функция. Это означает, что значит ее значения должны…повторяться! Синус начинается с 0, идет к 1, к 0, к -1, к 0 и так далее.

Давайте определим π как время, за которое синус поднимается с 0 до 1, и обратно возвращается к 0. Вау! Теперь и мы используем π без всяких окружностей!

• Синус — это плавное передвижение вперёд-назад
• π — это время движения синуса с 0 до 1 и обратно до 0
• n * π (0 * π, 1 * π, 2 * π и т.д.) — это момент времени, в котором синус равен 0
• 2 * π, 4 * π, 6 * π и т.д. — полные периоды синуса.

Ага! Вот почему π встречается в таком количестве формул! π не «принадлежит» окружностям больше, чем 0 или 1 — π касается возвращения синуса в центр! Окружность — это пример фигуры, которая повторяется и возвращается в центр каждые 2*π единиц. Но вибрации, скачки и т.д. возвращаются к центру каждый π!

Вопрос: если π — это половина естественного периода, почему оно длится вечно (является иррациональным числом)?

Можно я отвечу вопросом на вопрос, А почему длина диагонали «единичной окружности» равна квадратному корню из 2, который также уходит в бесконечность?

Но да, я понимаю, что это философски не удобно, когда природа ведет себя произвольно. Но что поделаешь…

Построение синусоиды в excel

Как построить график синусоиды в Excel.

Допустим имеется функция синусоиды, заданной уравнением y=sin4*x. Формула в Excel имеет вид:

=SIN(4*C4)

Требуется построить график функции.

Функция в данном случае непрерывная, поэтому по оси x ограничим интервалом от 1 до -1, шаг возьмём 0,1.

В итоги у нас должна получится таблица вида:

Переходим на вкладку Вставка -> Точечная с гладкими кривыми и маркерами.

Появится область графика, кликаем на белую область правым указателем мыши, выскакивает меню, далее Выбрать данные, появляется окно Выбора источника данных, выбираем весь диапазон данных нашей синусоиды в ячейках, затем Ок.

В итоги у нас получается график вида.

Также вид графика тоже можно настроить через конструктор и дополнительные инструменты.

трюки • приёмы • решения

Использование диаграмм Excel — хороший способ отображения графиков математических и тригонометрических функций. В этой статье описываются два метода построения графика функции: с одной переменной с помощью точечной диаграммы и с двумя переменными с помощью 3D-диаграммы.

Построение графиков математических функций с одной переменной

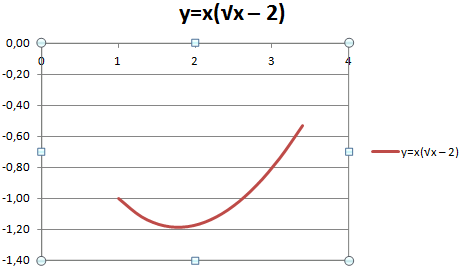
Точечная диаграмма (известная как диаграмма XY в предыдущих версиях Excel) отображает точку (маркер) для каждой пары значений. Например, на рис. 140.1 показан график функции SIN. На диаграмму наносятся рассчитанные значения у для значений х (в радианах) от -5 до 5 с инкрементом (приращением) 0,5. Каждая пара значений х и у выступает в качестве точки данных в диаграмме, и эти точки связаны линиями.

Рис. 140.1. Диаграмма представляет собой график функции SIN(x)

Функция выражается в таком виде: у = SIN(x) .

Соответствующая формула в ячейке В2 (которая копируется в ячейки, расположенные ниже) будет следующей: =SIN(A2) .

Чтобы создать эту диаграмму, выполните следующие действия.

1. Выделите диапазон А1:В22 .
2. Выберите Вставка ► Диаграммы ► Точечная ► Точечная с прямыми отрезками и маркерами.
3. Выберите макет диаграммы, который вам нравится, а затем настройте его.

Измените значения в столбце А для построения графика функции при различных значениях х. И, конечно, вы можете использовать любую формулу с одной переменной в столбце В. Вот несколько примеров, которые приводят к построению интересных графиков: =SIN(ПИ()*A2)*(ПИ()*A2) =SIN(A2)/A2 =SIN(A2^3)*COS(A2^2) =НОРМ.РАСП(A2;0;1;ЛОЖЬ)

Чтобы получить более точную диаграмму, увеличьте количество значений для построения графика и сделайте приращение в столбце А меньше.

Вы можете использовать онлайн наш файл примера графиков математических функций с одной переменной, расположенной в Excel Web Apps при помощи Skydrive, и внести свои данные (изменения не будут сохраняться) или скачать себе на компьютер, для чего необходимо кликнуть по иконке Excel в правом нижнем углу. Это бесплатно

Построение графиков математических функций с двумя переменными

Вы также можете строить графики функций, которые используют две переменные. Например, следующая функция рассчитывает z для различных значений двух переменных (х и у): =SIN($A2)*COS($B1)

На рис. 140.2 приведена поверхностная диаграмма, которая рассчитывает значение z для 21 значения х в диапазоне от -3 до 0 и для 21 значения у в диапазоне от 2 до 5. Для х и у используется приращение 0,15.

Рис. 140.2. Использование трехмерной поверхностной диаграммы для построения графика функции с двумя переменными

Значения х находятся в диапазоне А2:А22 , а значения у — в диапазоне B1:V1 .

Формула в ячейке В2 копируется в другие ячейки таблицы и имеет следующий вид: =SIN($A2)*C0S(B$1) .

Чтобы создать диаграмму, выполните приведенные ниже действия.

1. Выделите диапазон A1:V22 .
2. Выберите Вставка ► Диаграммы ► Другие ► Поверхность.
3. Выберите макет диаграммы, который вам нравится, а затем настройте его.

Пока значения х и у имеют равные приращения, вы можете задавать любую формулу с двумя переменными. Вам, возможно, потребуется настроить начальные значения и значение приращения для х и у. Для увеличения сглаживания используйте больше значений х и у при меньшем приращении. Вот другие формулы, которые вы можете попробовать: =SIN(КОРЕНЬ($A2^2+B$1^2)) =SIN($A2)*COS($A2*B$1) =COS($A2*B$1)

Функция SIN в Excel используется для вычисления синуса угла, заданного в радианах, и возвращает соответствующее значение.

Функция SINH в Excel возвращает значение гиперболического синуса заданного вещественного числа.

Функция COS в Excel вычисляет косинус угла, заданного в радианах, и возвращает соответствующее значение.

Функция COSH возвращает значение гиперболического косинуса заданного вещественного числа.

Покопаемся в расчётах

Давайте опишем синус с помощью вычислений. Как в случае с e, мы можем разбить синус на маленькие части:

• Начнем с 0 и дорастем до единичной скорости
• В каждый момент времени мы будем замедляться из-за отрицательного ускорения

И как обо всем этом думать? Посмотрите, как каждое наше действие изменяет расстояние от центра:

• Наш первый скачок увеличивает расстояние линейно: у (расстояние от центра) = х (затраченное время)
• В любой момент, мы чувствуем возвращающую силу -х. Мы интегрируем дважды, чтобы обратить отрицательное ускорение в расстояние:

Понимание того, как ускорение влияет на расстояние, похоже на наблюдение за тем, как прибавки влияют на ваш банковский счёт. «Прибавка» должна изменять ваш доход, а ваш доход изменяет состояние вашего банковского счёта (два интеграла «по команде»).

Так что после «х» секунд, мы уже догадаемся, что синус это «х» (начальный импульс) минус x^3/3! (эффект ускорения):

Что-то не так — синус не спадает! В случае с е мы видели, что «проценты приносят свои проценты», в случае с синусом происходит то же самое. «Возвращающая сила» меняет наше расстояние на -x^3/3!, что создает другую возвращающую силу. Рассмотрите пружину: если отпустить пружину с грузиком внизу, то толчок будет достаточно большим, чтобы создать другой толчок, который потянет грузик обратно вверх, а потом снова вниз. Ох уж эти неугомонные пружины!

Нам нужно рассмотреть каждую возвращающую силу:

• y = x — это наше изначальное движение, которое создает возвращающую силу удара:
• y = -x^3/3!, которая создает возвращающую силу удара:
• y = x^5/5!, которая создает возвращающую силу удара:
• y = -x^7/7!, которая создает возвращающую силу удара…

Точь-в-точь как е, синус можно описать бесконечным уравнением:

Я видел эту формулу много раз, но до меня дошел ее смысл только когда я представил синус как комбинацию начального импульса и возвращающих сил. Начальный импульс (y = x, растет вверх) в итоге превосходит возвращающая сила (которая толкает нас вниз), и эта сила в свою очередь постепенно компенсируется своей возвращающей силой (что снова толкает нас вверх), и так далее.

Пара интересных заметок:

• Рассматривайте «возвращающую силу» как «положительный или отрицательный процент». Так проще понять связь синуса и е в формуле Эйлера. Синус ведет себя как е, кроме моментов, когда он начинает зарабатывать отрицательный процент. Тут нам еще надо поучиться :).
• Для маленьких чисел «y = x» — неплохое предположение для синуса. Мы просто берем начальный импульс и игнорируем возвращающие силы.

График синуса и косинуса

Заметим, что координаты точек, лежащей на единичной окружности, варьируются в пределах от – 1 до 1. Это означает, что значение синуса и косинуса также может находиться только в интервале между этими числами. Получается, что область значения этих ф-ций – это промежуток .

Вычислить синус и косинус можно для абсолютно любого угла поворота, поэтому область определения этих тригонометрических ф-ций – вся числовая прямая, то есть промежуток (– ∞; + ∞).

Изучение графиков тригонометрических функций начнем с синуса. В тригонометрии при построении графика синуса принято по оси Ох откладывать значение угла в радианах, а не в градусах. Из-за этого в школьной тетради тяжело точно отметить точки, через которые проходит этот график. Например, возьмем угол, равный 90°. Его величина в радианах π/2, а sinπ/2 = 1. Получается, график должен пройти через точку (π/2; 1). Однако число π/2 – иррациональное, равное примерно 1,5708…, и точно отложить отрезок длиной π/2 невозможно.

Поэтому в учебных целях график строят приближенно (естественно, что на практике точный график можно построить с помощью компьютера с любой требуемой точностью). Считают, что величина π/2 примерно равна 1,5, то есть дроби 3/2. Если выбрать масштаб, при котором единице равны 2 клеточки, то π/2 – это 3 клеточки. Тогда π/6 – это одна клеточка, а π/3 – две.

Мы знаем, что

sin 0 = 0

sin π/6 = 1/2

sin π/2 = 1

Значит, график синуса должен проходить через точки (0; 0), (π/6; 1/2) и (π/2; 1). Отметим их на координатной плоскости:

С помощью некоторых соображений симметрии можно вычислить ещё несколько точек в диапазоне от 0 до 2π. Не будем перечислять их координаты, а просто отметим их на рисунке:

Теперь соединим их плавной кривой:

Мы получили график синуса на промежутке от 0 до 2π. Но ведь мы можем вычислить синус для любого другого угла! При этом мы используем тот факт, что углам, отличающимся на 2π (на один полный оборот), на единичной окружности соответствует одинаковая точка. То есть этим двум углам будут соответствовать точки на графике с одинаковой ординатой (координатой у), но абсциссами, отличающимися на 2π. Другими словами, точку графика можно перенести на 2π (то есть 12 клеточек) влево или вправо:

Перенести можно не одну точку, а сразу всё множество точек, лежащих между 0 и 2π:

Получили ещё два участка графика, на промежутках и . Эти участки также можно переместить влево и вправо. Продолжая этот процесс бесконечно, мы получим весь график у = sinx:

В результате мы получили кривую, которую называют синусоидой.

Теперь построим график косинуса. Мы знаем что

cos 0 = 1

cos π/3 = 1/2

cos π/2 = 1

Получается, что график должен проходить через точки (0;1), (π/3; 1/2) и (π/2; 0). Отметим их на плоскости:

Можно вычислить, используя симметрию на единичной окружности, ещё несколько точек, которые должны лежать на графике. Не приводя этих вычислений, просто отметим эти точки на плоскости:

Соединяем эти точки плавной линией:

Как и в случае с синусом, участок графика косинуса можно перенести на 2π (12 клеточек влево и вправо). В результате таких действий получим окончательный вид ф-ции у = cosх:

Можно заметить несколько особенностей полученных графиков. Во-первых, все точки обоих графиков лежат в «полосе» между прямыми у = 1 и у = – 1. Это следствие того, что и у синуса, и у косинуса область значений – это промежуток :

Во-вторых, график косинуса очень похож на синусоиду. Он имеет такую же форму, но просто смещен на π/2 (3 клеточки) влево. Это не случайно, в будущих уроках мы узнаем причину этого явления. Но, так как график косинуса – это просто смещенная синусоида, то термин «косинусоида» для его обозначения почти не используется – он просто избыточен.

В-третьих, графики обладают периодичностью. Они «повторяются» с периодом 2π. Дело в том, что углам, отличающимся друг от друга на 2π (то есть ровно на один полный поворот в 360°), на единичной окружности соответствует одна и та же точка. То есть справедливы формулы:

sin (x+ 2π) = sinx

cos (x+ 2π) = sinx

В-четвертых, можно заметить, что график косинуса симметричен относительно оси Ох, а график синуса симметричен относительно начала координат. Это значит, что синус является , а косинус – . Напомним, что ф-ция f(x) является нечетной, если справедливо условие

f(x) = – f(– x)

Если f(x) – четная ф-ция, то должно выполняться условие:

f(x) = f(– x)

Действительно, если отложить на единичной окружности углы α и (– α), то можно заметить, что их косинусы будут равны друг другу, и синусы окажутся противоположными:

Поэтому верны формулы:

sin (– α) = – sinα

cos (– α) = cosα

Рубрика «Вопросы и ответы»

Первый раз, изучая синусы, я упустил несколько вещей:

Синус вообще-то 1-мерный.

Синус движется в одном измерении. Правда. Мы часто рисуем синус, изменяющийся во времени, а иногда и «предмет», описывающий своим движением синус, тоже куда-то движется, но это уже опционально! Скачок в одном направлении — вполне себе полноценная волна синусоиды.

Окружности — это пример синусных волн.

Окружности и квадраты — это комбинации базовых элементов (синусов и прямых отрезков). Но окружности не являются основой синусоиды, как и квадрат не является составной частью прямой.

Что показывают значения синуса?

Синус принимает значения от -1 до 1. Он начинается с 0, возрастает до 1.0 (максимум), падает до -1.0 (минимум) и снова возвращается в нейтральную точку, к нулю. Я также вижу синус как процент от 100% (полный вперёд!) до -100% (полный обратный ход).

Что означает вводное значение ‘x’ в функции sin(x)?

Каверзный вопрос. Поскольку это цикл и х — вводный параметр, он означает, как далеко мы прошли по окружности.

Рассмотрим пример с линиями:

• Мы бродим по квадрату. За 10 секунд мы проходим каждую сторону.
• Спустя 1 секунду, вы прошли 10% от одной стороны
• Спустя 5 секунд, вы прошли одну сторону на 50%
• Через 10 секунд вы пройдете всю сторону.

В линейном движении есть парочка сюрпризов. Рассмотрим теперь синус (сфокусируемся на цикле «от 0 до максимума»):

• Мы путешествуем по синусоиде, стартуя с 0 (нейтральная точка) до 1.0 (максимум). И на этот путь у нас ушло 10 секунд.
• Спустя 5 секунд мы…прошли 70%! Синус очень быстрый на старте, и потихоньку замедляется к вершине. Так что большую часть пути мы пройдем за первые 5 секунд.
• И еще 5 секунд нам потребуется на то, чтобы пройти с 70% до 100% пути. А отрезок с 98% до 100% занимает почти целую секунду!

Несмотря на высокую начальную скорость, синус замедляет свой рост, так что мы очень плавно касаемся точки максимума и разворачиваемся назад. Эта плавность и делает синус синусом.

Если вам очень интересны подробности, нажмите «show stats» в симуляторе. Вы увидите процент выполнения полного цикла, мини-цикла (с 0 до 1.0) и текущее значение. Остановите движение (кнопка Stop), попереключайтесь между линейным и синусоидальным движением, чтобы сравнить значения.

Маленькая проверка: Что будет дальше, 10% линейного цикла или 10% синусного? Правильный ответ — синусного.

Помните, в самом начале синус максимально ускорен. Ко времени достижения 50% цикла, синус движется со средней скоростью линейного цикла и, более того, замедляется (пока не достигнет максимума и не развернется).

Так что x — это «количество вашего цикла». Какого цикла?

Зависит от контекста.

• Базовый вариант: ‘x’ — это градусы, и полный цикл состоит из 360 градусов
• Продвинутый вариант: ‘x’ — это радианы (они более натуральные!) и полный цикл составляет полный проход по единичной окружности (2*π радиан)

Поэкспериментируйте со значением х здесь:

Но опять же, циклы зависят от окружностей! Можем ли мы как-то вырваться из-под их тирании?

Определение 2: Бесконечный ряд

Я спрятал слона в комнате: как мы вообще вычисляем синус? Мой калькулятор, что, каждый раз рисует окружность и замеряет его?

Рад вам поведать, как можно вычислить синус без окружностей.

Синус — это ускорение в сторону, противоположную тому, где вы находитесь.

Пользуясь нашим примером с банковским счётом: представьте, что ваш шеф каждую неделю решил менять вашу зарплату на сумму, противоположную текущей на вашем банковском счёте. Если у вас сейчас есть 50 рублей, на следующей неделе шеф выдаст на 50 рублей меньше. Конечно, поскольку ваш доход будет 75 рублей, вы всё еще будете в плюсе (75 — 50) но в итоге ваш баланс уменьшится, поскольку «прибавки» шефа превзойдут ваши доходы.

Но не отчаивайтесь! Как только баланс становится отрицательным (скажем, у вас -50 рублей), ваш босс выдаст вам на целых 50 рублей больше. Затем снова баланс станет отрицательным (с его ростом шеф выдает всё меньше денег), и так будет продолжаться постоянно. Баланс будет то положительный, то нулевой, то отрицательный.

Этот пример также поясняет, почему в нейтральной точке (в 0) скорость синуса максимальна: когда вы на максимуме, вы начинаете падать и собирать всё больше «отрицательных прибавок», которые довольно быстро тянут вас к 0. После прохождения 0 вы начинаете получать наиболее значительные положительные прибавки и замедляетесь., потому что как только уходите в плюс, шеф опять начинает отнимать от вашей зарплаты.

Между прочим: поскольку синус — это ускорение, обратное к вашему текущему положению, а окружность сделана из горизонтальной и вертикальной синусоиды… вы поняли! Круговое движение может быть описано как «постоянное движение в направлении, противоположном текущей позиции, по направлению к горизонтальному и вертикальному центру».

Особенности использования тригонометрических функций в Excel

Синтаксис функции SIN:

=SIN(число)

Синтаксис функции SINH:

=SINH(число)

Синтаксис функции COS:

=COS(число)

Синтаксис функции COSH:

>=COSH(число)

Каждая из приведенных выше функций принимает единственный аргумент число, который характеризует угол, заданный в радианах (для SIN и COS) или любое значение из диапазона вещественных чисел, для которого требуется определить гиперболические синус или косинус (для SINH и COSH соответственно).

Примечания 1:

1. Если в качестве аргумента любой из рассматриваемых функций были переданы текстовые данные, которые не могут быть преобразованы в числовое значение, результатом выполнения функций будет код ошибки #ЗНАЧ!. Например, функция =SIN(“1”) вернет результат 0,8415, поскольку Excel выполняет преобразование данных там, где это возможно.
2. В качестве аргументов рассматриваемых функций могут быть переданы логические значения ИСТИНА и ЛОЖЬ, которые будут интерпретированы как числовые значения 1 и 0 соответственно.
3. Все рассматриваемые функции могут быть использованы в качестве формул массива.

Примечения 2:

1. Синус гиперболический рассчитывается по формуле: sinh(x)=0,5*(ex-e-x).
2. Формула расчета косинуса гиперболического имеет вид: cosh(x)=0,5*( ex+e-x).
3. При расчетах синусов и косинусов углов с использованием формул SIN и COS необходимо использовать радианные меры углов. Если угол указан в градусах, для перевода в радианную меру угла можно использовать два способа:

• Функция РАДИАНЫ (например, =SIN(РАДИАНЫ(30)) вернет результат 0,5;
• Выражение ПИ()*угол_в_градусах/180.

В Microsoft Excel 2007 достаточно просто строить диаграммы и графики различных видов. Поэтому построить график какой-нибудь стандартной математической функции в Excel не составит особого труда. В этом обучающем материале по информатике будет рассмотрен процесс построения графика функции синуса в Microsoft Excel 2007.

Описывать процесс создания мы будем на примере Microsoft Excel 2007 (уже устаревшая, но очень хорошая версия программы). Процесс построения графика в более свежем Microsoft Excel 2010 будет отличаться лишь в некоторых деталях.

Электронные таблицы Excel изначально были созданы компанией Microsoft для вычислений. Результаты наших вычислений мы будем применять в качестве исходных данных для построения графика.

Насколько быстр синус?

Я вас немного запутал. Сначала я сказал: «представьте, что синусу нужно 10 секунд, чтобы добраться с 0 до максимума». А сейчас я говорю, что ему надо π секунд, чтобы добраться с 0 до максимума и обратно спуститься к 0. Что происходит?

• sin(x) — это базовая синусная волна, которой действительно требуется π единиц времени, чтобы пройти путь с 0 до максимума и опять до 0 (или 2*π, чтобы обойти свой полный период)
• sin(2x) — это синусоида, которая движется вдвое быстрее
• sin(x/2) — это синусоида, которая движется вдвое медленее базовой

Так что мы используем sin(n*x) , чтобы сделать синус, который будет двигаться так быстро, как нам нужно. Очень часто слово «синусоида» используется для указания общей формы волны, а не конкретной скорости.