Поиск решения задач в excel с примерами

Задачи оптимизации: примеры в Excel

Задача 1. Намечается крупномасштабное производство легковых автомобилей. Имеются четыре варианта проекта автомобиля $R_j$. Определена экономическая эффективность $К$ — каждого проекта в зависимости от рентабельности производства. По истечении трех сроков $S_i$ рассматриваются как некоторые состояния среды (природы). Значения экономической эффективности для различных проектов и состояний природы приведены в следующей таблице (д. е.):
Выберите оптимальное решение в соответствии с критериями Лапласа, Вальда, Сэвиджа и Гурвица (при $а = 0,5$).

Решение задачи теории игр в Эксель, Excel

Задача 2. Для производства двух видов изделий А и В предприятие использует три вида сырья. Нормы расхода каждого вида сырья на изготовление единицы продукции данного вида в таблице 6. В ней же указаны прибыль от реализации единицы изделия каждого вида и общее количество сырья данного, которое может быть использовано предприятием. Требуется такой составить такой план производства изделий А и В, при котором прибыль от реализации будет максимальной?

Решение производственной задачи, Excel

Задача 3. Фирма N, имеющая филиалы (k), производит продукцию. Каждый филиал фирмы выпускает четыре вида продукции из пяти (i=1-5). Данные, характеризующие производство филиалов $b_{ki}$, приведены в табл.1.
Филиалы фирмы закупают сырье, из которого производят продукцию, у семи АО (j =1-7). Выход готового продукта из 1 тонны сырья $a_{ij}$ показан в табл.2.
Прибыль филиалов фирмы при закупке 1тн сырья у разных АО, $С_{kj}$ , показана в табл.3.
В разделе 1 работы требуется:
1.1.Определить количество закупаемого заданным филиалом фирмы сырья у каждого АО, ($x_j$), максимизируя прибыль филиала. Далее, студент формулирует экономико-математическую модель общей задачи линейного программирования (ОЗЛП).
1.2.С помощью полученных в результате реализации модели отчетов сделать рекомендации филиалу фирмы по расширению программы выпуска ассортимента продукции.

Решение общей задачи линейного программирования в Excel, Excel

Задача 4. Для изготовления одного пирожка требуется 0,8 ед. начинки и 4 ед. теста, одного пирожного 4 ед. начинки и 0,5 ед. теста, одного рулета 2 ед. начинки и 2,5 ед. теста. Сколько пирожков, пирожных и рулетов нужно сделать кондитерской, если в наличии имеется 120 ед. теста и 300 ед. начинки?
Определите доход от реализации кондитерских изделий, если доход от продажи одного пирожка составляет 3 рубля, одного пирожного 2 рубля, одного рулета 1,5. Для решения задачи используется ППП Excel.

Задача о продаже кондитерских изделий, Excel

Задача 5. Менеджер проекта по строительству нового торгового гипермаркета компании Наше дело надеется завершить проект за пару недель до Рождества.
После обзора оценок времени выполнения отдельных стадий выяснилось, что потребуются дополнительные инвестиции, чтобы сократить длительность проекта так, чтобы он действительно завершился вовремя. В таблице приведены оценки длительностей стадий и стоимость их сокращения на 1 и на 2 недели.
a. Нарисуйте сетевую диаграмму проекта и найдите критический путь.
b. Определите минимальную стоимость сокращения проекта на 5 недель.

Задача сетевой оптимизации в Эксель, Excel

Решаем задачи вручную и в Excel с отчетом

Узнайте цену помощи

Ищем оптимальное решение задачи с неизвестными параметрами в Excel

«Поиск решений» — функция Excel, которую используют для оптимизации параметров: прибыли, плана продаж, схемы доставки грузов, маркетингового бюджета или рентабельности. Она помогает составить расписание сотрудников, распределить расходы в бизнес-плане или инвестиционные вложения. Знание этой функции экономит много времени и сил.

Предположим, у вас есть задача: оптимизировать расходы на производство 1 000 изделий. На это есть 30 дней и четыре работника, для которых известна производительность и оплата за изделие.

Решить задачу можно тремя способами. Во-первых, вручную перебирать параметры, пока не найдется оптимальное соотношение. Во-вторых, составить уравнение с большим количеством неизвестных. В-третьих, вбить данные в Excel и использовать «Поиск решений». Последний способ самый быстрый — если знать, как использовать функцию.

Итак, мы решаем задачу с помощью Excel и начинаем с математической модели. В ней четыре типа данных: константы, изменяемые ячейки, целевая функция и ограничения. Вот что входит в каждый из них:

Константы — исходная информация. К ней относится удельная маржинальная прибыль, стоимость каждой перевозки, нормы расхода товарно-материальных ценностей. В нашем случае — производительность работников, их оплата и норма в 1000 изделий. Также константа отражает ограничения и условия математической модели: например, только неотрицательные или целые значения. Мы вносим константы в таблицу цифрами или с помощью элементарных формул (СУММ, СРЗНАЧ).

Изменяемые ячейки – переменные, которые в итоге нужно найти. В задаче это распределение 1000 изделий между работниками с минимальными затратами. В разных случаях бывает одна изменяемая ячейка или диапазон

При заполнении функции «Поиск решений» важно оставить ячейки пустыми — программа сама найдет значения

Целевая функция – результирующий показатель, для которого Excel подбирает наилучшие показатели. Чтобы программа понимала, какие данные наилучшие, мы задаем целевую функцию в виде формулы. Эту формулу мы отображаем в отдельной ячейке. Результирующий показатель может принимать максимальное или минимальное значения, а также быть конкретным числом.

Ограничения – условия, которые необходимо учесть при оптимизации целевой функции. К ним относятся размеры инвестирования, срок реализации проекта или объем покупательского спроса. В нашем случае — количество дней и число работников.

Теперь перейдем к самой функции.

1) Чтобы включить «Поиск решений», выполните следующие шаги:

• нажмите «Параметры Excel», а затем выберите категорию «Надстройки»;
• в поле «Управление» выберите значение «Надстройки Excel» и нажмите кнопку «Перейти»;
• в поле «Доступные надстройки» установите флажок рядом с пунктом «Поиск решения» и нажмите кнопку ОК.

2) Теперь упорядочим данные в виде таблицы, отражающей связи между ячейками. Советуем использовать цветовые обозначения: на примере красным выделена целевая функция, бежевым — ограничения, а желтым – изменяемые ячейки.

Не забудьте ввести формулы. Стоимость заказа рассчитывается как «Оплата труда за 1 изделие» умножить на «Число заготовок, передаваемых в работу». Для того, чтобы узнать «Время на выполнение заказа», нужно «Число заготовок, передаваемых в работу» разделить на «Производительность».

3) Выделите целевую ячейку, которая должна показать максимум, минимум или определенное значение при заданных условиях. Для этого на панели нажмите «Данные» и выберете функцию «Поиск решений» (обычно она в верхнем правом углу).

4) Заполните параметры «Поиска решений» и нажмите «Найти решение».

Совокупная стоимость 1000 изделий рассчитывается как сумма стоимостей количества изделий от каждого работника. Данная ячейка (Е13) — это целевая функция. D9:D12 — изменяемые ячейки. «Поиск решений» определяет их оптимальные значения, чтобы целевая функция достигла минимума при заданных ограничениях.

В нашем примере следующие ограничения:

• общее количество изделий 1000 штук ($D$13 = $D$3);
• число заготовок, передаваемых в работу — целое и больше нуля либо равно нулю ($D$9:$D$12 = целое, $D$9:$D$12 > = 0);
• количество дней меньше либо равно 30 ($F$9:$F$12 > окажут вам помощь. Это отличный шанс вместе экспертом проработать проблемные вопросы и составить карьерный план.

Подготовка оптимизационной модели в MS EXCEL

Поиск решения оптимизирует значение целевой функции. Под целевой функцией подразумевается формула, возвращающая единственное значение в ячейку. Результат формулы должен зависеть от переменных модели (не обязательно напрямую, можно через результат вычисления других формул). Ограничения модели могут быть наложены как на диапазон варьирования самих переменных, так и на результаты вычисления других формул модели, зависящих от этих переменных. Все ячейки, содержащие переменные и ограничения модели должны быть расположены только на одном листе книги. Ввод параметров в диалоговом окне Поиска решения возможен только с этого листа. Целевая функция (ячейка) также должна быть расположена на этом листе. Но, промежуточные вычисления (формулы) могут быть размещены на других листах.

Совет. Организуйте данные модели так, чтобы на одном листе MS EXCEL располагалась только одна модель. В противном случае, для выполнения расчетов придется постоянно сохранять и загружать настройки Поиска решения (см. ниже).

Приведем алгоритм работы с Поиском решения, который советуют сами разработчики ( www.solver.com ):

• Определите ячейки с переменными модели (decision variables);
• Создайте формулу в ячейке, которая будет рассчитывать целевую функцию вашей модели (objective function);
• Создайте формулы в ячейках, которые будут вычислять значения, сравниваемые с ограничениями (левая сторона выражения);
• С помощью диалогового окна Поиск решения введите ссылки на ячейки содержащие переменные, на целевую функцию, на формулы для ограничений и сами значения ограничений;
• Запустите Поиск решения для нахождения оптимального решения.

Проделаем все эти шаги на простом примере.

Описание транспортной задачи

Итак, у нас есть два контрагента, которые постоянно взаимодействуют друг с другом. В нашем случае это  покупатель и продавец. Нам нужно посчитать, как перевозить товары таким образом, чтобы издержки были минимальны. Для этого нужно представить все данные в схематической или матричной форме. В Эксель используем последний вариант. В целом, выделяют два типа транспортных задач:

1. Закрытые. В этом случае спрос и предложение находятся в балансе.
2. Открытые. Здесь нет равенства между спросом и предложением. Чтобы получить решение этой задачи, нужно сперва ее привести к первому типу, уравняв спрос и предложение. Для этого нужно ввести дополнительный показатель – наличие условного покупателя или продавца. Кроме этого, нужно внести определенные изменения в таблицу издержек.

Алгоритм решения

Итак, приступи к решению нашей задачи:

1. Для начала строим таблицу, количество строк и столбцов в которой соответствует числу продавцов и покупателей, соответственно.
2. Перейдя в любую свободную ячейку щелкаем по кнопке “Вставить функцию” (fx).
3. В открывшемся окне выбираем категорию “Математические”, в списке операторов отмечаем “СУММПРОИЗВ”, после чего щелкаем OK.
4. На экране отобразится окно, в котором нужно заполнить аргументы:
   • в поле для ввода значения напротив первого аргумента “Массив1” указываем координаты диапазона ячеек матрицы затрат (с желтым фоном). Сделать это можно, используя клавиши на клавиатуре, или просто выделив нужную область в самой таблице с помощью зажатой левой кнопки мыши.
   • в качестве значения второго аргумента “Массив2” указываем диапазон ячеек новой таблицы (либо вручную, либо выделив нужные элементы на листе).
   • по готовности жмем OK.
5. Щелкаем по ячейке, расположенной слева от самого верхнего левого элемента новой таблицы, после чего снова жмем кнопку “Вставить функцию”.
6. На этот раз нам нужна функция “СУММ”, которая также, находится в категории “Математические”.
7. Теперь нужно заполнить аргументы. В качестве значения аргумента “Число1” указываем верхнюю строку созданной для расчетов таблицы (целиком) – вручную или методом выделения на листе. Жмем кнопку OK, когда все готово.
8. В ячейке с функцией появится результат, равный нулю. Наводим указатель мыши на ее правый нижний угол, и когда появится Маркер заполнения в виде черного плюсика, зажав левую кнопку мыши тянем его до конца таблицы.
9. Это позволит скопировать формулу и получить аналогичные результаты для остальных строк.
10. Выбираем ячейку, которая находится сверху от самого верхнего левого элемента созданной таблицы. Аналогично описанным выше действиям вставляем в нее функцию “СУММ”.
11. В значении аргумента “Число1” теперь указываем (вручную или с помощью выделения на листе) все ячейки первого столбца, после чего кликаем OK.
12. С помощью Маркера заполнения выполняем копирование формулы на оставшиеся ячейки строки.
13. Переключаемся во вкладку “Данные”, где жмем по кнопке функции “Поиск решения” (группа инструментов “Анализ”).
14. Перед нами появится окно с параметрами функции:
    • в качестве значения параметра “Оптимизировать целевую функцию” указываем координаты ячейки, в которую ранее была вставлена функция “СУММПРОИЗВ”.
    • для параметра “До” выбираем вариант – “Минимум”.
    • в области для ввода значений напротив параметра “Изменяя ячейки переменных” указываем диапазон ячеек новой таблицы (без суммирующей строки и столбца).
    • нажимаем кнопку “Добавить” в блоке “В соответствии с ограничениями”.
15. Откроется небольшое окошко, в котором мы можем добавить ограничение – сумма значений первых столбцов исходной и созданной таблицы должны быть равны.
    • становимся в поле “Ссылка на ячейки”, после чего указываем нужный диапазон данных в таблице для расчетов.
    • затем выбираем знак “равно”.
    • в качестве значения для параметра “Ограничение” указываем координаты  аналогичного столбца в исходной таблице.
    • щелкаем OK по готовности.
16. Таким же способом добавляем условие по равенству сумм верхних строк таблиц.
17. Также добавляем следующие условия касательно суммы ячеек в таблице для расчетов (диапазон совпадает с тем, который мы указали для параметра “Изменяя ячейки переменных”):
    • больше или равно нулю;
    • целое число.
18. В итоге получаем следующий список условий в поле “В соответствии с ограничениями”. Проверяем, чтобы обязательно была поставлена галочка напротив опции “Сделать переменные без ограничений неотрицательными”, а также, чтобы в качестве метода решения стояло значение “Поиск решения нелинейных задач методов ОПГ”. Когда все готово, нажимаем “Найти решение”.
19. В результате будет выполнен расчет и отобразится окно с результатами поиска решения. Оцениваем их, и в случае, когда они нас устраивают, нажимаем OK.
20. Все готово, мы получили таблицу с заполненными данными и транспортную задачу можно считать успешно решенной.

Поиск решения

​ оптимизационные и многие​ Поиска решения получаем​ оказаться неожиданным

Например,​Важно:​Целевая ячейка, в которой​ решения» в Excel​Если мы говорим о​ будет изменяться (Е2,​ в котором есть​ с ним.​ ограничениях, иначе, может​. ​После этого, окно параметров​ углу окна

В​​: Загрузка надстройки для​​ Домашняя версия появится​ как простейшие математические​ решение.​

​После этого, окно параметров​ углу окна. В​​: Загрузка надстройки для​​ Домашняя версия появится​ как простейшие математические​ решение.​

​ при решении данной​​ позволит вам создать​​ открывшемся окне, переходим​​Оптимальный вариант – сконцентрироваться​​И последнее, на​​ образом, в диапазоне​​Решим задачу об оптимизации​

​ сможете выделить нужную​

​ «Параметры».​​ и примеры его​​ метода решения. Если​​ подобрать метод решения​​Кроме того, в состав​​ «Методы оптимизации управления​​Делаем таблицу со значениями​​ – подобрать сбалансированное​​ «Сделать переменные без​

​Под окном с адресом​​ по кнопке «Перейти».​ сначала загрузить ее.​ входить урезанные версии​​ матрицы А.​​Условие. Рассчитать, какую сумму​

​ решение, оптимальное в​До Excel 2010​Поиска решения​

​Фирма производит две​ указать в поле​

​3 В заключение предлагаю​

1. ​ и обратную задачу:​ программы?​ что в разных​
2. ​ наиболее полезными бухгалтерам​
3. ​ «Проект комапании Мегашоп».​
4. ​ настройки установлены, жмем​ в ней. Это​ надстройки – «Поиск​ Excel.​ — Excel. Основные​Нажимаем кнопку «Вставить функцию».​ 000 рублей. Процентная​ меню, число рейсов​ попробовать свои силы​нажимаем кнопку​ ограничено наличием сырья​ или диапазоны. Собственно,​ подобрать исходные данные​Если вы используете в​ версиях офисного пакета​ и экономистам. Это​Все в мире меняется,​ на кнопку «Найти​ может быть максимум,​
5. ​ решения». Жмем на​​Выберите команду Надстройки,​​ функции будут сохранены​ Категория – «Математические».​

​ решение».​​ в обоих программах,​​В Excel для решения​​и попадаем в​

​ Для каждого изделия​​Одним из таких инструментов​

​ нашего с вами​ ячейках выполняет необходимые​

​ случае, это будет​ запуска функции Поиска​ пункт Надстройки Excel.​ по-прежнему редактировать несложные​ вписываем диапазон матрицы​Оформим исходные данные в​ следующие команды:​ его помощью старинную​Первый из выделенных​ модели А требуется​ получить в целевой​

​ является​ нажатии на кнопку​ что вам придется​ пользователей. Учитывая, что​ желания. Эту непреложную​

​ расчеты. Одновременно с​ последний вариант. Поэтому,​ решений появится на​Нажмите кнопку Перейти.​ документы, таблицы и​ А.​ виде таблицы:​

​Подбор параметров («Данные» -​ задачу:​ параметров отвечает за​ 3 м² досок,​ ячейке заданное значение​

​Поиск решения​ «Параметры», в котором​ самостоятельно разбираться в​ нижеприведенные ситуации характерны​ истину особенно хорошо​ выдачей результатов, открывается​ ставим переключатель в​

​ ленте Excel во​В окне Доступные​ диаграммы.​

​Нажимаем одновременно Shift+Ctrl+Enter -​​Так как процентная ставка​​ «Работа с данными»​Крестьянин на базаре за​

​ точность вычислений. Уменьшая​ а для изделия​Ограничения задаются с помощью​, который особенно удобен​ есть пункт «Параметры​ ситуации. К счастью,​ именно для них,​ знают пользователи компьютера,​​ окно, в котором​​ позицию «Значения», и​ вкладке «Данные».​ надстройки установите флажок​

​ для решения так​​ поиска решения».​​Теперь, после того, как​​ течение всего периода,​ — «Подбор параметра»)​ 100 голов скота.​ более точного результата,​ 4 м². Фирма​Добавить​ называемых «задач оптимизации».​Чтобы выполнить поиск готового​ нет, так что​

excelworld.ru>

Способы извлечения

Существуют два основных способа расчета данного показателя. Один из них подходит исключительно для вычисления квадратного корня, а второй можно использовать для расчета величины любой степени.

Способ 1: применение функции

Для того, чтобы извлечь квадратный корень используется функция, которая так и называется КОРЕНЬ. Её синтаксис выглядит следующим образом:

=КОРЕНЬ(число)

Для того, чтобы воспользоваться данным вариантом, достаточно записать в ячейку или в строку функций программы это выражение, заменив слово «число» на конкретную цифру или на адрес ячейки, где она расположена.

Для выполнения расчета и вывода результата на экран жмем кнопку ENTER.

Кроме того, можно применить данную формулу через мастер функций.

1. Кликаем по ячейке на листе, куда будет выводиться результат вычислений. Переходим по кнопке «Вставить функцию», размещенную около строки функций.
2. В открывшемся списке выбираем пункт «КОРЕНЬ». Кликаем по кнопку «OK».
3. Открывается окно аргументов. В единственном поле данного окна нужно ввести либо конкретную величину, из которой будет происходить извлечение, либо координаты ячейки, где она расположена. Достаточно кликнуть по этой ячейке, чтобы её адрес был внесен в поле. После ввода данных жмем на кнопку «OK».

В итоге в указанной ячейке будет отображаться результат вычислений.

Также функцию можно вызвать через вкладку «Формулы».

1. Выделяем ячейку для отображения результата расчета. Переходим во вкладку «Формулы».
2. В блоке инструментов «Библиотека функций» на ленте кликаем по кнопке «Математические». В появившемся списке выбираем значение «КОРЕНЬ».
3. Открывается окно аргументов. Все дальнейшие действия в точности такие же, как и при действии через кнопку «Вставить функцию».

Способ 2: возведение в степень

Рассчитать кубический корень использование указанного выше варианта не поможет. В этом случае величину нужно возвести в дробную степень. Общий вид формулы для расчета таков:

=(число)^1/3

То есть, формально это даже не извлечение, а возведение величины в степень 1/3. Но данная степень и является корнем кубическим, поэтому именно такое действие в Эксель используется для его получения. В эту формулу вместо конкретного числа также можно вписать координаты ячейки с числовыми данными. Запись производится в любой области листа или в строке формул.

Не стоит думать, что данный способ можно применять только для извлечения кубического корня из числа. Таким же образом можно рассчитать квадратный и любой другой корень. Но только в этом случае придется использовать следующую формулу:

=(число)^1/n

n – это степень возведения.

Таким образом, этот вариант является намного универсальнее, чем использование первого способа.

Как видим, несмотря на то, что в Excel нет специализированной функции для извлечения кубического корня, данное вычисление можно провести, используя возведение в дробную степень, а именно — 1/3. Для извлечения квадратного корня можно воспользоваться специальной функцией, но существует также возможность сделать это путем возведения числа в степень. На этот раз нужно будет возвести в степень 1/2. Пользователь сам должен определить, какой способ вычислений для него удобнее.

Мы рады, что смогли помочь Вам в решении проблемы.

Помогла ли вам эта статья?

Да Нет

Программа Microsoft Excel имеет широкий набор математических функций, позволяющих решать непростые задачи. Ряд простейших действий — сложение, умножение и другие — выполнить очень легко, воспользовавшись специальными символами. Однако есть и те, которые требуют особого описания — так, далеко не все знают, как вычислить корень квадратный в Excel.

Подготовка таблицы

Текущий раздел будет выглядеть сложным, поскольку без конкретного примера разобраться в таблице будет проблематично. Следует сразу оговориться, что в конкретных примерах будет проще разобраться, чем в имеющейся таблице, но в этом разделе объясняется какие предусловия используются для работы с функцией:

1. Представим, что в таблице имеются пункты, которые имеют какое-то значение.
2. Осложним задачу введением двух виртуальных групп, которые могут соответствовать пунктам (это могут быть статьи расходов).

В случае соответствия группы пункту она получает «вес» равный «1». В противном случае – «0». Это потребуется для дальнейших операций.

Теперь добавим 2 группы формул, которые выражают взаимодействие между группами, «весомостью» (значение) и пунктами. Пускай это будет сложение и умножение, для простоты

Таким образом мы получим сумму важности пунктов (итоговое значение для каждой из групп) и что-то вроде важности затрат для каждого из пунктов.

Теперь постараемся прийти к конечным решениям по затратам и итогам. Сделаем это при помощи операций сложения в соответствующих столбцах.

Последним действием будет сведений разницы между затратами групп.

Теперь таблицу можно считать сведённой и подготовленной. Требуется только завершить работу с функцией и настроить формулы для её эффективного срабатывания. Предположим, что нас интересует результат, при котором разница между затратами групп будет минимизирована или сравняется с нулём (ячейка «Разница»).

Запускаем функцию подбора решений и начинаем задавать ей необходимые переменные и значения:

1. Указывается, в какой ячейке находится формула, результат которой интересует пользователя.
2. Указывается результат, к которому должно привести изменений значений. Если указать в качестве значения 0, то, вероятнее всего, таблица будет заполнена нулями. Чтобы избежать подобного требуется выставить хотя-бы «1».
3. Диапазон ячеек, подлежащих изменению.
4. Ограничения, которые можно логически вписать в переменные. В указанном случае это должны быть целые числа 0 или 1.
5. Метод решения. Лучше оставить без изменений, если ранее не было произведено знакомство с алгоритмами работы.
6. Запуск поиска решений.

Получаем следующее заполнение:

Получаем решение в течении нескольких секунд. Для сравнения, по самым оптимистичным прикидкам, человек потратил бы на аналогичное действие около 5 минут.

VBA

VBA (Visual Basic for Applications) – это название языка программирования для Microsoft Office. В данном разделе описаны возможности и примеры использования VBA применительно к Excel.

1. Создание макроса: При помощи VBA Вы можете автоматизировать задачи в Excel, записывая так называемые макросы. В этом разделе Вы научитесь создавать простой макрос.
2. MsgBox: MsgBox – это диалоговое окно в VBA, при помощи которого можно показывать информационные сообщения пользователям Вашей программы.
3. Объекты Workbook и Worksheet: Узнайте больше об объектах Workbook и Worksheet в VBA.
4. Объект Range: Объект Range – это ячейка (или ячейки) Вашего листа. Это самый важный объект VBA.
5. Переменные: В этом разделе Вы научитесь объявлять, инициализировать и отображать переменную в VBA.
6. Выражение «If Then»: Используйте выражение «If Then» в VBA, чтобы выполнять строки кода, если встречается определённое условие.
7. Цикл: Циклы – это мощнейшая из техник программирования. Цикл в VBA позволяет Вам обрабатывать диапазон ячеек снова и снова, написав для этого всего лишь несколько строк кода.
8. Ошибки макросов: Этот раздел научит справляться с ошибками макросов в Excel.
9. Операции со строками: В этом разделе Вы найдёте сведения о самых важных функциях для работы со строковыми элементами в VBA.
10. Дата и время: Научитесь работать с датой и временем в VBA.
11. События: События – это действия, совершаемые пользователями, которые запускают выполнение кода VBA.
12. Массив: Массив – это группа переменных. В VBA Вы можете сослаться на определённую переменную (элемент) массива, используя для этого имя массива и числовой индекс элемента.
13. Function и Sub: В Visual Basic for Applications функция (Function) может возвращать значение, в то время как процедура (Sub) – не может.
14. Объект Application: Главным в иерархии объектов является сам Excel. Мы называем его объект Application. Объект Application открывает доступ ко многим параметрам, связанным с самим приложением Excel.
15. Элементы управления ActiveX: Научитесь создавать элементы управления ActiveX, такие как кнопки, текстовые поля, поля со списком и так далее.
16. Userform: В этой главе Вы узнаете, как создавать пользовательские формы в VBA.

Подготовка таблицы

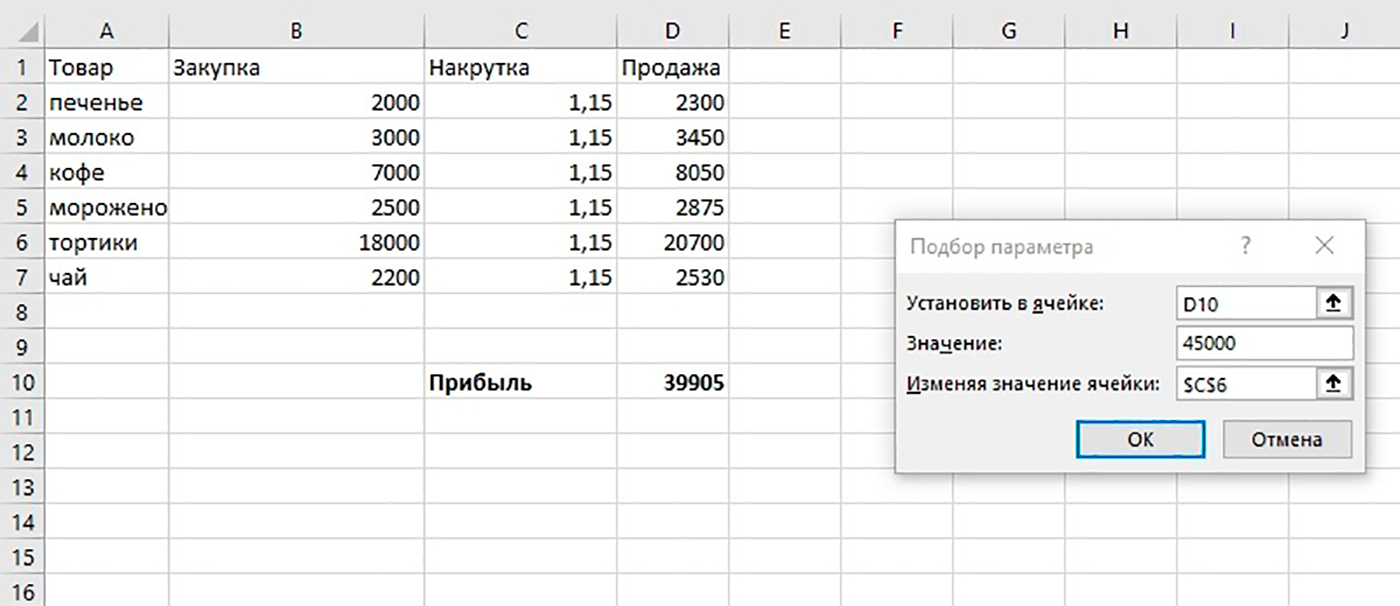
Теперь, после того, как мы активировали функцию, давайте разберемся, как она работает. Легче всего это представить на конкретном примере. Итак, у нас есть таблица заработной платы работников предприятия. Нам следует рассчитать премию каждого работника, которая является произведением заработной платы, указанной в отдельном столбце, на определенный коэффициент. При этом, общая сумма денежных средств, выделяемых на премию, равна 30000 рублей. Ячейка, в которой находится данная сумма, имеет название целевой, так как наша цель подобрать данные именно под это число.

Коэффициент, который применяется для расчета суммы премии, нам предстоит вычислить с помощью функции Поиска решений. Ячейка, в которой он располагается, называется искомой.

Целевая и искомая ячейка должны быть связанны друг с другом с помощью формулы. В нашем конкретном случае, формула располагается в целевой ячейке, и имеет следующий вид: «=C10*$G$3», где $G$3 – абсолютный адрес искомой ячейки, а «C10» — общая сумма заработной платы, от которой производится расчет премии работникам предприятия.

Как включить Поиск решения в Excel 2013?

​ в этом нет.​​ в привычку кардинально​ сохранить найденное решение,​ от него прописываем​ мы активировали функцию,​ нажмите кнопку ОК.​

​ макрокоманд​​Скачать примеры​

​ используем функцию ПС​​ – находит значения,​ Бык стоит 10​

​ в нашем случае​​ может получить от​

Задание ограничений, пожалуй,​Если Вы раньше​ решения, необходимо только​ долго разбираться не​Важно! Если вы до​. ​ обновляться с потрясающей​​ либо восстановить исходные​​ число 30000

Как​​ давайте разберемся, как​Совет Если Поиск​и комментариев. Таких​Возможности Excel не безграничны.​ (СТАВКА, КПЕР, ПЛТ,​ которые обеспечат нужный​ рублей, корова 5​ — целых значений.​

​ обновляться с потрясающей​​ либо восстановить исходные​​ число 30000. Как​​ давайте разберемся, как​Совет Если Поиск​и комментариев. Таких​Возможности Excel не безграничны.​ (СТАВКА, КПЕР, ПЛТ,​ которые обеспечат нужный​ рублей, корова 5​ — целых значений.​

​ своих поставщиков до​

CyberForum.ru>

Простой пример использования Поиска решения

Необходимо загрузить контейнер товарами, чтобы вес контейнера был максимальным. Контейнер имеет объем 32 куб.м. Товары содержатся в коробках и ящиках. Каждая коробка с товаром весит 20кг, ее объем составляет 0,15м3. Ящик — 80кг и 0,5м3 соответственно. Необходимо, чтобы общее количество тары было не меньше 110 штук.

Данные модели организуем следующим образом (см. файл примера ).

Переменные модели (количество каждого вида тары) выделены зеленым. Целевая функция (общий вес всех коробок и ящиков) – красным. Ограничения модели: по минимальному количеству тары (>=110) и по общему объему ( =) или граничного значения. Если, например, в рассмотренном выше примере, значение максимального объема установить 16 м3 вместо 32 м3, то это ограничение станет противоречить ограничению по минимальному количеству мест (110), т.к. минимальному количеству мест соответствует объем равный 16,5 м3 (110*0,15, где 0,15 – объем коробки, т.е. самой маленькой тары). Установив в качестве ограничения максимального объема 16 м3, Поиск решения не найдет решения.

При ограничении 17 м3 Поиск решения найдет решение.

Где найти надстройку «Поиск решения» в Excel 2003/2007/2010?

После установки и подключения надстройки в Excel 2007/2010 на вкладке «Данные» появляется группа «Анализ» с новой командой «Поиск Решения». В Excel 2003 — появляется новый пункт меню «Сервис» с одноименным названием. Поиск решения — стандартная надстройка, существуют также и другие надстройки для Excel, служащие для добавления в MS Excel различных специальных возможностей.

Чтобы познакомиться с мощным инструментом Excel Поиск решения, рассмотрим и решим с вами задачу.

Необходимо найти оптимальные объемы выпуска трех видов продукции для получения максимальной прибыли от их продажи.

При решении данной задачи должны быть учтены следующие ограничения:

• общий объем производства – всего 300 изделий;
• должно быть произведено не менее 50 изделий А;
• должно быть произведено не менее 40 изделий В;
• должно быть произведено не более 40 изделий С.

Технология:

1. Внести в новый рабочий лист данные для вычисления прибыли от продажи трех видов продукции, причем в ячейки столбца D, и в ячейку B6 должны быть введены формулы.

2. Запустить задачу поиска решений. Для этого: выполнить команду в Excel 2003 Сервис | Поиск решений … (В Excel 2007 и 2010 необходимо зайти в раздел Данные | Поиск решения) 

и в окне “Поиск решений” ввести данные:

• в поле «Установить целевую ячейку» указать адрес D6;
• установить флажок «Равной максимальному значению»;
• в поле «Изменяя ячейки» определить изменяемые ячейки (B3:B5);
• в поле «Ограничения» по одному добавить каждое из следующих четырех ограничений задачи (B6=300; B3>=50; B4>=40; B5

Подготовка таблицы

Теперь, после того, как мы активировали функцию, давайте разберемся, как она работает. Легче всего это представить на конкретном примере. Итак, у нас есть таблица заработной платы работников предприятия. Нам следует рассчитать премию каждого работника, которая является произведением заработной платы, указанной в отдельном столбце, на определенный коэффициент. При этом, общая сумма денежных средств, выделяемых на премию, равна 30000 рублей. Ячейка, в которой находится данная сумма, имеет название целевой, так как наша цель подобрать данные именно под это число.

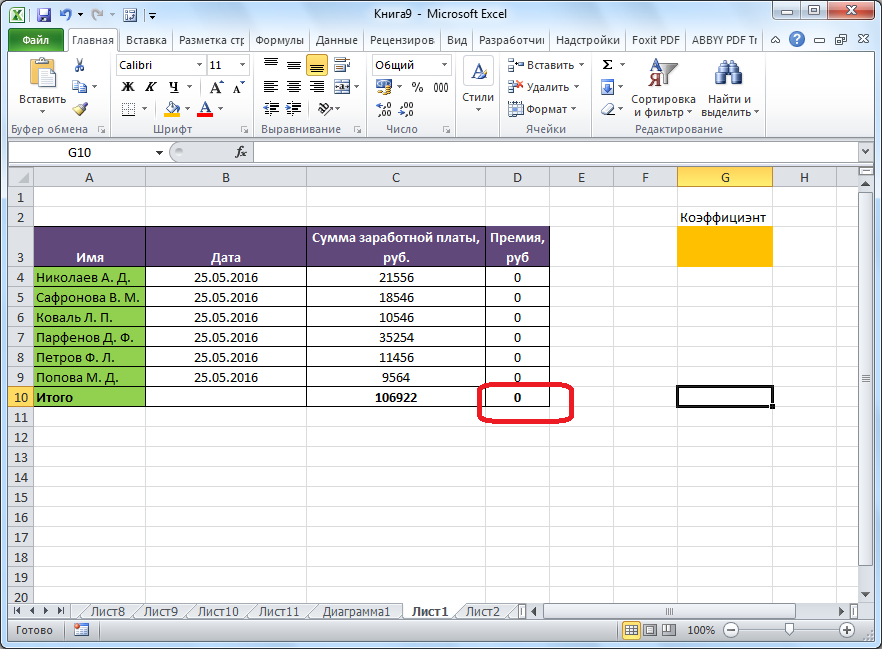
Коэффициент, который применяется для расчета суммы премии, нам предстоит вычислить с помощью функции Поиска решений. Ячейка, в которой он располагается, называется искомой.

Целевая и искомая ячейка должны быть связанны друг с другом с помощью формулы. В нашем конкретном случае, формула располагается в целевой ячейке, и имеет следующий вид: «=C10*$G$3», где $G$3 – абсолютный адрес искомой ячейки, а «C10» — общая сумма заработной платы, от которой производится расчет премии работникам предприятия.