Сложный процент. формула сложного процента для вклада. расчет сложных процентов

Содержание:

Примеры сложных процентов в инвестициях
Деление числа на 100
Начисление процентов несколько раз в год
Формула сложного процента
Сложные проценты по вкладу
Плюсы и минусы компаундирования
Примеры сложных процентов в инвестициях
Как даже с 1 000 рублей в кармане создать пассивный доход к пенсии
Формулы расчета
Школьные задачи на сложные проценты
Среднегодовая доходность
- - Плавная доходность лучше всплесков
Эффективная процентная ставка по вкладу
- Как было до 2021 года
- Как стало с 2021 года
В чем отличие
Простые проценты
- Примеры задач на простые проценты
Как рассчитать сложный процент по вкладу в банке

Примеры сложных процентов в инвестициях

Можно смело сказать, что каждый рубль отложенный сегодня принесёт десятки рублей через 10 лет за счёт постоянного реинвестирования прибыли. Подобным образом разбогатели многие миллиардеры (Уоррен Баффет).

Обратите внимание, что эффект заметен со временем все сильнее и в конце кривая сложных процентов приобретает экспоненциальный характер, в то время как простые проценты растут линейно. Рассмотрим на примерах этот принцип

2.1. Пример: инвестируем ежемесячно в банк под 8% (срок 10 лет)

Если откладывать ежемесячно по 10 тысяч рублей «под подушку» или просто на банковский счёт, то через 10 лет (120 месяцев) сумма будет 1.2 млн рублей (120 умножаем на 10 тыс).

Если же откладывать эти деньги на банковский вклад под 8% годовых, то сумма по истечению 10 лет будет значительно больше: 1 851 738 рублей. Чистый доход от процентов 641 738 рублей (чуть больше 50% за все время).

Новички по ошибке могут получить неправильную сумму, если просто прибавить 8% к отложенной сумме, но это неверно. Сложный процент можно посчитать лишь на онлайн калькуляторе или самостоятельно с помощью длительных вычислений.

Расчёты на калькуляторе сложных процентов:

Выписка по балансу:

Примечание

В некоторые периоды можно найти ставку на вкладах гораздо выше 8% и доход был бы в таком случае был заметно больше.

2.2. Пример: инвестируем в банк под 8% (срок 20 лет)

Теперь увеличим срок нашего инвестирования с 10 лет до 20 лет. Мы будем также откладывать по 10 тысяч рублей и всю полученную прибыль реинвестировать. Теперь по истечению срока сумма будет 5 938 760 рублей вместо 2 400 000. Чистый доход от процентов 3 528 760. Эта сумма больше всех суммарных вложений в 1.5 раза (150% прибыли за все время)!

Это наглядный пример того, что чем больший период мы рассматриваем, тем заметнее будет действие сложных процентов.

2.3. Пример: инвестируем в ценные бумаги под 12% (срок 20 лет)

Последний пример депозита. Откладываем по 10 тысяч рублей ежемесячно на протяжении 20 лет, но теперь мы инвестируем деньги в акции и небольшую часть в облигации.

Как показала реальная история, такой инвестиционный портфель в среднем за год приносит 12% с учётом дивидендов от акций при самой простой стратегии «купи и держи».

Итого, сумма на конец срока: 9 999 681 рублей. Чистый доход 7 589 681 рублей. И это не результат везения, не фантастика, а очень реальные цифры дохода, которые доступны каждому лицу. По факту можно даже получить и больше и даже за более короткий срок, если выйти с рынка на его пике, а докупиться в конце цикла падения, но для подобных «маневров» необходимы основы трейдинга и немного времени на совершение торговых операций.

Хочу подчеркнуть, что мы рассмотрели реальные варианты без каких-либо везений и прочее. Такого результата добьется каждый, кто просто вложит в ценные бумаги и не будет дергаться и пытаться что-то ещё сделать. Такая стратегия называется: пассивное индексное инвестирование.

Примечание

При инвестировании в зарубежные акции доход был бы ещё больше (где-то в два раза), поскольку по статистике рубль обесценивается к доллару примерно на 100% каждые 20 лет.

Также важно откладывать в начале как можно больше. Это сильно повышает будущую доходность

Теперь, понимая силу сложных процентов, поговорим о том, во что лучше всего вложить деньги, чтобы получать пассивный доход. Какие конкретно варианты инвестирования существуют, каковы их риски и преимущества можно прочитать:

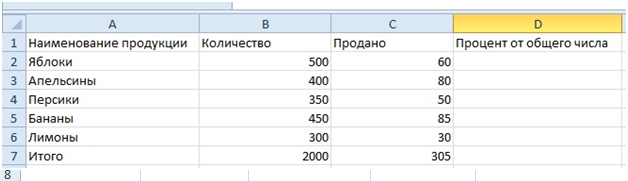
Деление числа на 100

При делении на 100 получается 1% от этого числа. Это правило можно использовать по-разному. Например, чтобы узнать процент от суммы, нужно умножить их на размер 1%. А чтобы перевести известное значение, следует разделить его на размер 1%. Этот метод отлично помогает в вопросе, как перевести целое число в проценты.

Представьте, что вы пришли в магазин за шоколадом. Обычно он стоит 250 рублей, но сегодня скидка 15%. Если у вас есть дисконтная карта магазина, шоколад обойдется вам в 225 рублей. Чем будет выгоднее воспользоваться: скидкой или картой?

Как решаем:

Переведем 15% в рубли:
250 : 100 = 2,5 — это 1% от стоимости шоколада,
значит 2,5 * 15 = 37,5 — это 15%.
250 — 37,5 = 212,5.
212,5 < 225.

Ответ: выгоднее воспользоваться скидкой 15%.

Начисление процентов несколько раз в год

В рассмотренном выше случае капитализация производится 1 раз в год. При капитализации m раз в год формула наращения для сложных процентов выглядит так: S = Р*(1+i/m)^(n*m) i/m – это ставка за период. На практике обычно используют дискретные проценты (проценты, начисляемые за одинаковые интервалы времени: год (m=1), полугодие (m=2), квартал (m=4), месяц (m=12)).

В MS EXCEL вычислить наращенную сумму к концу срока вклада по сложным процентам можно разными способами.

Рассмотрим задачу : Пусть первоначальная сумма вклада равна 20т.р., годовая ставка = 15%, срок вклада 12 мес. Капитализация производится ежемесячно в конце периода.

Способ 1. Вычисление с помощью таблицы с формулами Это самый трудоемкий способ, но зато самый наглядный. Он заключается в том, чтобы последовательно вычислить величину вклада на конец каждого периода. В файле примера это реализовано на листе Постоянная ставка .

За первый период будут начислены проценты в сумме =20000*(15%/12) , т.к. капитализация производится ежемесячно, а в году, как известно, 12 мес. При начислении процентов за второй период, в качестве базы, на которую начисляются %, необходимо брать не начальную сумму вклада, а сумму вклада в конце первого периода (или начале второго). И так далее все 12 периодов.

Способ 2. Вычисление с помощью формулы Наращенных процентов Подставим в формулу наращенной суммы S = Р*(1+i )^n значения из задачи. S = 20000*(1+15%/12)^12 Необходимо помнить, что в качестве процентной ставки нужно указывать ставку за период (период капитализации). Другой вариант записи формулы – через функцию СТЕПЕНЬ() =20000*СТЕПЕНЬ(1+15%/12; 12)

Способ 3. Вычисление с помощью функции БС(). Функция БС() позволяет определить будущую стоимость инвестиции при условии периодических равных платежей и постоянной процентной ставки, т.е. она предназначена прежде всего для расчетов в случае аннуитетных платежей . Однако, опустив 3-й параметр (ПЛТ=0), можно ее использовать и для расчета сложных процентов. =-БС(15%/12;12;;20000)

Или так =-БС(15%/12;12;0;20000;0)

Примечание . В случае переменной ставки для нахождения Будущей стоимости по методу сложных процентов используется функция БЗРАСПИС() .

Формула сложного процента

Годовая процентная ставка в любом случае указывается в договоре депозита. Формула расчета сложных процентов депозита выглядит следующим образом:

SUM = X * (1 + p*d/y) n

где:

SUM – конечная сумма;
X – начальная сумма;
p – процентная ставка (процентов годовых / 100) по вкладу, например, если ставка 5%, то p = 5 / 100 = 0,05;
d – период (количество дней), по итогам которого происходит капитализация (начисляются проценты), например, если капитализация ежемесячная, то d = 30 дней, если капитализация раз в 3 месяца, то d = 90 дней;
y – количество дней в календарном году (365 или 366);
n – количество периодов, лет (месяцев, кварталов).

Для вкладчиков, которым сложно производить математические расчеты, создан так называемый калькулятор сложных процентов, интерактивная система, позволяющая рассчитать прибыль по депозиту при капитализации процентов.

Прибыль по вкладу при капитализации (начислении сложных процентов) находится в зависимости от:

размера процентной ставки;
продолжительности расчетного периода;
суммы первоначального взноса на счет;
частоты начисления процентов.

Чем дольше длится расчетный период, тем выше прибыль депозитного вклада.

Сложные проценты по вкладу

Отличие простых процентов от сложных на самом деле довольно большое. При выборе депозитного продукта наверняка каждому приходилось слышать о таком понятии, как капитализация. То есть это та схема начисления прибыли, при которой начисленная прибыль причисляется к телу депозита, а на него в будущем снова начисляется доход.

Отсюда можно сделать вывод, что капитализация позволяет получить большую прибыль по сравнению с простым процентом. Чтобы наглядно в этом убедиться рассмотрим формулу расчета сложных процентов, а выглядеть она будет следующим образом: B=(K×H×P/N)/100, где:

B – размер начисленной прибыли;
K – тело депозита;
H – годовая ставка;
P – количество дней, в течение которых происходит капитализация;
N – число дней в году.

Чтобы наглядно понять, как именно будет рассчитываться сложный процент. Рассмотрим простой пример. Сумма депозита 50000 рублей процентная ставка в год 7%, капитализация осуществляется ежемесячно, срок действия договора один год. Произведем расчет прибыли за первый месяц пользования депозитом: B=(50000×7×30/365)/100=287,6 рублей – это прибыль за первый месяц. В следующем периоде расчет будет выглядеть следующим образом: B=(50287,6×7×31/365)/100=298,9 рублей.

Из вышеприведенного примера можно сделать вывод, что капитализация позволяет получать с каждым месяцем большую прибыль по сравнению с предыдущим

Вот только при выборе депозитного предложения обязательно обратить внимание, с какой периодичностью осуществляется капитализация процентов, чем чаще, тем больше выгоды получает клиент

Плюсы и минусы компаундирования

Альберт Эйнштейн назвал это финансовое явление восьмым чудом света или величайшим изобретением человека. Недостатком капитализации является то, что иногда она может работать против потребителей. Речь идет о клиентах, которые имеют ссуды с высокими процентными ставками. Например, задолженность по кредитным картам.

Пример: Анализируем остаток по кредитной карте в размере 20 000 дол по процентной ставке 20%. Она начисляется ежемесячно, приводит к совокупной ставке в размере 4 388 дол за один год или около 365 дол в месяц.

С другой стороны, этот процесс приносит клиентам пользу. Когда речь заходит об инвестициях, капитализация становится мощным фактором создания богатства. Экспоненциальный рост за счет сложного процента важен для смягчения факторов, которые разрушают благосостояние. К ним относят:

рост стоимости жизни;
инфляция;
снижение покупательной способности;

Паевые инвестиционные фонды предлагают инвесторам один из самых простых способов воспользоваться преимуществами сложных дивидендов. Выбор реинвестирования дивидендов приводит к приобретению большего количества акций фонда. Они получены от взаимного фонда. Со временем накапливаются более сложные проценты. Цикл покупки большего количества акций будет продолжать способствовать росту стоимости инвестиций в фонд.

Рассмотрим следующий пример:

Инвестиция в паевой инвестиционный фонд с начальными 5000 долларов и годовой прибавкой 2400 долларов. При средней годовой доходности в 12% за 30 лет будущая стоимость фонда составляет 798 500 дол. Сложный процент — это разница между денежными средствами и фактической будущей стоимостью инвестиций. Капитализация вносится в инвестиции.

В этом случае при внесении 77 000 дол или совокупного взноса всего в 200 дол в месяц в течение 30 лет сложный процент составляет 721 500 дол будущего остатка. Доходы от сложных процентов облагаются налогом, если деньги не находятся на защищенном от налогов счете.

Защищенный счет обычно облагается налогом по стандартной ставке, связанной с налоговой шкалой налогоплательщика.

Как рассчитать сложные проценты

Примеры сложных процентов в инвестициях

Кривые доходности при сложных и простых процентах

Пример: инвестируем ежемесячно в банк под 8% (срок 10 лет)

Если же откладывать эти деньги на банковский вклад под 8% годовых, то сумма по истечению 10 лет будет значительно больше 1 851 738 рублей. Чистый доход от процентов 641 738 рублей (чуть больше 50% за все время). Новички по ошибке могут получить неправильную сумму, если просто прибавить 8% к отложенной сумме, но это неверно. Сложный процент можно посчитать лишь на онлайн калькуляторе или самостоятельно с помощью длительных вычислений.

Расчёты на калькуляторе сложных процентов:

Выписка по балансу:

Примечание

Пример: инвестируем в банк под 8% (срок 20 лет)

Пример: инвестируем в ценные бумаги под 12% (срок 20 лет)

Последний пример. Откладываем также по 10 тысяч рублей ежемесячно на протяжении 20 лет, но теперь мы инвестируем деньги в акции и небольшую часть в облигации. Как показала реальная история, такой инвестиционный портфель в среднем за год приносит 12% с учетом дивидендов от акций при самой простой стратегии «купи и держи».

Итого, сумма на конец срока: 9 999 681 рублей. Чистый доход 7 589 681 рублей. И это не результат везения, не фантастика, а очень реальные цифры дохода, которые доступны каждому лицу! По факту можно даже получить и больше и даже за более короткий срок, если выйти с рынка на его пике, а докупиться в конце цикла падения, но для подобных «маневров» необходимы основы трейдинга и немного времени на совершение торговых операций.

Мы рассмотрели реальные варианты без каких-либо везений и прочее. Такого результата добьется каждый, кто просто вложит в ценные бумаги и не будет дергаться и пытаться что-то еще сделать. Такая стратегия называется: купи и держи.

Примечание

При инвестировании в зарубежные акции доход был бы еще больше (где-то в два раза), поскольку по статистике рубль обесценивается к доллару примерно на 100% каждые 20 лет.

Также важно откладывать в начале как можно больше. Это сильно повышает будущую доходность

Как даже с 1 000 рублей в кармане создать пассивный доход к пенсии

Пенсионный возраст увеличили, накопительную пенсию заморозили, регулярно проводят пенсионную реформу и меняют условия. Все эти хаотичные телодвижения говорят только о том, что у руководства нет четкого плана действий и видения, как же должна начисляться пенсия в нашей стране.

Какой вывод простому гражданину нужно сделать из всего этого? Только один – накопить на пенсию самостоятельно. И поможет в этом сложный процент. На конкретных расчетах посмотрим, как даже с 1 000 ₽ в месяц создать пассивный доход. Но для начала замечательная сказка из книги Бодо Шефера “Мани, или Азбука денег”.

Жил-был когда-то крестьянин. Каждое утро он ходил в курятник, чтобы взять на завтрак яйцо, которое снесла его курица. Но однажды он нашел в гнезде не обычное яйцо, а золотое. Сначала он не мог в это поверить. Возможно, кто-то решил над ним зло подшутить. Но ювелир, которому он принес показать яйцо, подтвердил, что оно из чистого золота. Крестьянин выгодно продал яйцо и устроил большой праздник.

На следующее утро он пошел в курятник раньше, чем обычно. В гнезде опять лежало золотое яйцо. Так продолжалось несколько дней. Но крестьянин был жадным и хотел побыстрее разбогатеть. Он злился на свою курицу, потому что “глупая птица” не могла объяснить ему, как она умудряется нести золотые яйца. Ему казалось, что тогда он мог бы и сам нести золотые яйца. Тогда у него было бы каждый день по два яйца. И однажды крестьянин так сильно разозлился, что вбежал в курятник и зарезал свою курицу. Некому стало нести золотые яйца.

Мораль этой сказки такова: нельзя резать курицу, несущую золотые яйца. Но чтобы получать золотые яйца, надо сначала завести курочку. Этим вы и должны заняться как можно скорее. Время – друг инвестора и враг того, кто откладывает на потом создание личного капитала.

Пример 1. Необходимо рассчитать, сколько денег нужно накопить, чтобы жить на пассивный доход через какое-то количество лет. Допустим, мы хотим на пенсии ежемесячно получать 50 000 ₽. Учтем инфляцию 4 %.

Ставку доходности примем равной 10 %. Ее размер зависит от состава инвестпортфеля. Если решили копить в облигациях, то закладывать надо меньший %. Если составить сбалансированный портфель из разных инструментов (например, ETF, акции и облигации отдельных эмитентов, золото), то 10 % – очень консервативная оценка. На практике получается значительно больше.

Расчет без учета инфляции: 50 000 * 12 месяцев / 0,1 = 6 000 000 ₽. Для учета инфляции воспользуемся онлайн-калькулятором. Необходимо накопить уже 10 000 000 ₽.

Пример 2. Есть начальный капитал 50 000 ₽ с ежемесячным вложением равной суммы: 1 000 ₽, 5 000 ₽ и 10 000 ₽. Доходность – 10 %, примем ежегодное начисление %. Сколько накопим через 10, 20, 30 и 40 лет?

Сумма ежемесячных взносов	Срок накопления
10 лет	20 лет	30 лет	40 лет
1 000 ₽	320936,22	1023674,99	2846398,39	7574073,45
5 000 ₽	1085932,6	3772874,97	10742111,47	28818516,12
10 000 ₽	2042178,08	7209374,94	20611752,84	55374069,46

Какие выводы мы можем сделать из этих расчетов:

Накопить на пассивный доход в 50 000 ₽ в месяц мы сможем, откладывая 5 000 ₽ в течение 30 лет. Если инвестируем по 10 000 ₽, то уже примерно через 23 года можно выходить на пенсию.
С ежемесячными 1 000 ₽ нужно довольствоваться меньшей суммой пассивного дохода. Например, чтобы получать ежемесячно 35 000 ₽, надо накопить 7 000 000 ₽. Из таблицы видно, что только через 40 лет достигнем этого. А вот для ежемесячной прибавки к пенсии в 20 000 ₽ понадобится накопить 4 000 000 ₽ за 35 лет.

Поиграйте своими цифрами в любом финансовом калькуляторе сложных процентов. У кого-то начальная или ежемесячная сумма будет больше, кто-то рассмотрит меньший или больший срок и т. д.

Формулы расчета

Раз есть сложный, значит, есть и простой процент. Несправедливо, если мы не разберем младшего брата нашего героя.

Простой процент

Простой процент каждый расчетный период (месяц, квартал, год) начисляется только на первоначальную сумму. Никакого эффекта “снежного кома” он не дает. Сумма увеличивается медленно.

Формула расчета:

S_N = S_П * (1 + % ст * N), где

S_N – сумма в конце периода N;
S_П – первоначальная сумма капитала;
% ст – процентная ставка (доход);
N – расчетный период.

Формула справедлива, если речь идет о начислении дохода раз в год. Например, положили на счет 100 000 ₽ под 10 % годовых на 10 лет. В конце срока получите: 100 000 * (1 + 0,1 * 10) = 200 000 ₽.

В реальной жизни понятие простого % применяется, например, в экономических расчетах по банковским вкладам без учета капитализации. В договоре обязательно указывается годовая процентная ставка. Проценты начисляются за каждый день нахождения денег на вкладе. А получать доход вкладчик может ежемесячно, ежеквартально или раз в год.

В этом случае формула примет вид:

S_N = S_П * (1 + % ст * Д / 365), где

Д – количество полных дней нахождения денег на депозите.

Например:

Положили на счет 100 000 ₽ под 10 % годовых на 91 день. В конце срока получите: 100 000 * (1 + 0,1 * 91 / 365) = 102 493,15 ₽.
На 180 дней: 100 000 * (1 + 0,1 * 180 / 365) = 104 931,51 ₽.
На 2 года (730 дней): 100 000 * (1 + 0,1 * 730 / 365) = 120 000 ₽.

Сложный процент с начислением дохода 1 раз в год

По методу сложных процентов при начислении дохода 1 раз в год будущая сумма определяется по формуле:

S_N = S_П * (1 + % ст)N

Пример. В банк положили 100 000 ₽ под 10 % годовых на 2 года. Будущая стоимость вклада составит: 100 000 * (1 + 0,1)2 = 121 000 ₽.

Сложный процент с начислением дохода чаще, чем 1 раз в год

Доход может начисляться ежемесячно, ежеквартально или 2 раза в год. Формула меняется:

S_N = S_N * (1 + % ст / К)N*К, где

К – частота начисления дохода (12, 4 или 2 раза в год).

Пример. В банк положили 100 000 ₽ под 10 % годовых на 2 года с ежемесячным начислением процентов. Будущая стоимость вклада составит: 100 000 * (1 + 0,1/12)24 = 122 039,1 ₽.

Школьные задачи на сложные проценты

Например, возьмем задачи из учебника для 9 класса авторов А.Г. Мерзляк, В.Б. Полонский, М.С. Якир «Аглгебра». (Номер в скобках)

Задача 1. (556) Костюм стоил 600 грн. После того как цена была снижена дважды, он стал стоить 432 грн., Причем процент снижения второй был в 2 раза больше, чем в первый раз. На сколько процентов каждый раз снижалась цена?

Решение: Для упрощения вычислений обозначим X – первая скидка; X/2 – вторая скидка. Для вычисления неизвестной X составляем уравнение Упрощаем, и сводим к квадратному уравнению и решаем Первый решение не имеет физического смысла, второй учитываем при вычислениях. Значение 0,2 соответствует снижению на 0,2*100%=20% после первой скидки, и X/2 =10% после второй скидки.

Задача 2. (557) Определенный товар стоил 200 грн. Сначала его цену повысили на несколько процентов, а затем снизили на столько же процентов, после чего стоимость его стала 192 грн. На сколько процентов каждый раз происходила смена цены товара?

Решение: Поскольку проценты одинаковы, то обозначаем изменении цены товара через X. На основе условия задачи получим уравнение Его упрощение приведет к решению уравнения откуда корни приобретут значений Первая значение отвергаем, оно меняет суть задачи (сначала имеем снижение, а затем рост процентов, противоречит условию). Второе при пересчете составит 0,2*100%=20% процентов.

Задача 3. (558) Вкладчик положил в банк 4000 грн. За первый год ему начислена определенный процент годовых, а второго года банковский процент увеличен на 4%. На конец второго года на счете стало 4664 грн. Сколько процентов составила банковская ставка в первый год?

Решение: Обозначим через X – увеличение вклада в первый год, тогдаX+4/100%=X+0,04 начисления во второй год. По условию задачи составляем уравнение для определения неизвестной X После упрощений получим квадратное уравнение вида Вычисляем дискриминант и корни уравнения Первый корень отбрасываем, второй соответствует ставке в 6% годовых.

Задача 4. (564) В сосуде 12 кг кислоты. Часть кислоты отлили и долили до прежнего уровня водой. Затем снова отлили столько же, как и в первый раз, и долили водой до прежнего уровня. Сколько литров жидкости отливали каждый раз, если в результате получили 25-процентный раствор кислоты?

Решение: Обозначим через X – часть кислоты, которую отливали. После первого раза ее осталось 12-X, а процентное содержание кислоты После второй попытки содержание кислоты в сосуде составило. Разведя водой до 12 кг, процентное содержание составляло 25%. Составляем уравнение Упрощаем проценты и избавляемся знаменателей Решаем квадратное уравнение Условии задачи удовлетворяет второе решение, а это значит, что каждый раз отливали 6 кг жидкости. На этом знакомство со сложными процентами завершается. На практике Вам встретятся как простые так и сложные задачи. При проблемах с вычисления сложных процентов обращайтесь к нам, мы поможем Вам в решении задач.

Среднегодовая доходность

Для сравнения разных способов инвестиций на дистанции нам необходимо уметь считать среднегодовую доходность наших инвестиций. Формула при условии, что мы один раз инвестировали деньги и потом получили некий результат:

Пример: в 2014 году мы инвестировали на биржу 100 000 рублей. Через 3 года у нас на счету стало 285 000 рублей. Рассчитаем среднегодовую доходность за три года:

Самопроверка:

Экономический смысл: если бы выбирали между банком и биржей по доходности, то нам нужно было бы найти банк, который предлагает ставку в размере 41,78% или выше на протяжении 3 лет ежегодно.

Формула для расчета среднегодовой доходности, если нам известны результаты инвестиций по годам:

Пример: в первый год инвестор заработал 15%, во второй потерял -10% и в третий заработал 29%. Какова его среднегодовая доходность?

Несмотря на два очень удачных года среднегодовая доходность инвестора оказалась на уровне всего лишь 10,11%.

Периоды падения очень отрицательно сказываются на среднегодовой доходности!

Давайте ещё раз сделаем самопроверку и окончательно поймем экономический смысл. Посчитаем сначала с учетом ежегодной доходности по каждому году результат инвестирования:

Разница в 15 рублей получилась за счет округления 10,11%.

Плавная доходность лучше всплесков

Многие инвесторы (особенно новички) гонятся за огромными доходностями, получают их в один год и терпят “незначительные” убытки в следующий год. Давайте рассмотрим ещё один показательный случай из практики, что “медленные инвесторы” в итоге выигрывают:

Инвестор 1 получил доходность в первый год +90%, во второй год убыток в размере -21% и в третий год доходность в размере +15%.

Инвестор 2 получил доходность в первый год +21%, во второй год +32% и в третий год всего лишь +9%.

Кто заработал больше?

1.9*0.79*1.15 = 1.72615

Среднегодовая доходность первого 19,96%.

1.21*1.32*1.09 = 1.784112

Среднегодовая доходность второго 21,29%.

“Сверхдоходность” в 90% не спасла “быстрого” инвестора. Его итоговый результат оказался ниже, чем результат работы “плавного” инвестора.

Минусы вредны для портфеля. Если портфель упал на 20%, то ему надо заработать 25%, чтобы хотя бы восстановиться.

Сколько нужно зарабатывать после падений для восстановления первоначальной суммы на счете

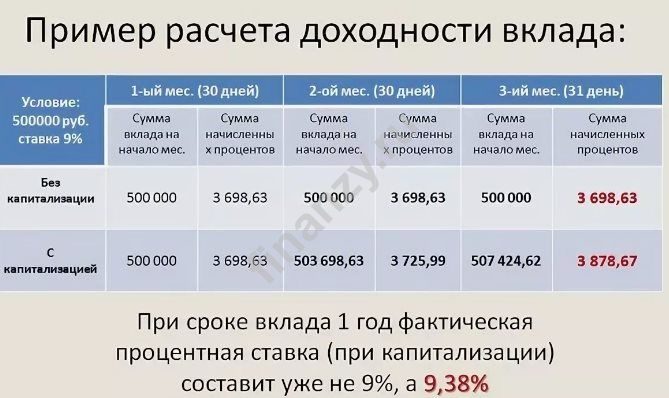
Эффективная процентная ставка по вкладу

Эта характеристика актуальна только для вкладов с капитализацией процентов. В связи с тем, что проценты не выплачиваются а идут на увеличение суммы вклада, очевидно, что если ежемесячно возрастает сумма вклада, то и вновь начисленные на эту сумму проценты также будут выше, как и конечный доход.

Если рассчитать, сколько процентов было начислено к начальной сумме к концу срока вклада, эта величина и будет являться эффективной процентной ставкой.

Формула расчета эффективной ставки:

где
N — количество выплат процентов в течение срока вклада,T — срок размещения вклада в месяцах.

Эта формула не универсальна. Она подходит только для вкладов с капитализацией 1 раз в месяц, период которых содержит целое количество месяцев. Для других вкладов (например вклад на 100 дней) эта формула работать не будет.

Однако есть и универсальная формула для рассчета эффективной ставки. Минус этой формулы в том, что получить результат можно только после рассчета процентов по вкладу.

Эта формула подходит для всех вкладов, с любыми сроками и любой периодичностью капитализации. Она просто считает отношение полученного дохода к начальной сумме вклада, приводя эту величину к годовым процентам. Лишь небольшая погрешность может присутствовать здесь, если период вклада или его часть выпала на високосный год.

Именно этот метод используется для рассчета эффективной ставки в представленном здесь депозитном калькуляторе.

Как было до 2021 года

Налог начислялся в случаях, если ставка по вкладу превышала ключевую на 5 и более процентов. Размер налога был 35% и 30% для резидентов и нерезидентов соответственно. Начислялся он не на весь доход во вкладу, а только на разницу между доходом, вычисленным по пороговой ставке (ключевая ставка + 5%) и реально полученным доходом.

Как стало с 2021 года

Налоговая ставка теперь 13% для всех.
Введена необлагаемая сумма дохода. Все, что выше — облагается налогом. Количество вкладов не имеет значения, считается общая сумма на всех вкладах.
Необлагаемый доход рассчитывается следующим образом:
Налог платится 1 раз в год за все вклады.
ФНС рассчитывает сумму налога самостоятельно и направляет уведомление.
Срок уплаты — 1 декабря года, следующего за расчетным.

В качестве примера возьмем 2021 год.

У Васи есть 2 вклада в разных банках. В первом банке 500 000 руб. под 5%, во втором банке 800 000 руб под 4%.
Ключевая ставка ЦБ на 1 января 2021 года была 4.25%.
Сумма необлагаемого дохода едина для всех вкладов и составляет 1 000 000 × 4.25% = 42 500 руб. С этой суммы налог платить не нужно.
Доход по вкладам васи за год составит: в первом банке — 25 000 руб., во втором — 32 000 руб. Всего — 57 000 руб.
Разница между фактическим и необлагаемым доходом составит 57 000 — 42 500 = 14 500 руб. Это тот доход, с которого необходимо заплатить НДФЛ.
Размер НДФЛ = 14 500 × 13% = 1 885 руб.

В чем отличие

На самом деле система начисления процентов по вкладам сильно различается в первую очередь по той причине, что с капитализацией процентов выгода депозита может быть значительно выше, нежели при простой системе. Потому что при простой системе прибыль растет в арифметической прогрессии, а при сложной в геометрической. Чтобы наглядно в этом убедиться, ниже приведена схема сложных процентов в сравнении со схемой простых процентов.

Схема сложных процентов в сравнении со схемой простых процентов

Но, в этом вопросе также есть подводные камни

Условия банковских вкладов строго индивидуальны, поэтому при выборе депозитного продукта в первую очередь обратите внимание на количество периодов капитализации за весь срок действия договора. Например, банк указывает, что по вашему депозитному договору предусмотрена капитализация процентов, но она осуществляется 1 раз в 6 месяцев, то есть первый доход, вы получите спустя полгода после заключения соглашения с банком

При этом вы решили разместить средства лишь на 3 месяца, соответственно, вы получите свои средства раньше, чем банк проведет капитализацию процентов и в данном случае целесообразней выбрать простой расчет процент по вкладу.

На самом деле понять, в чем состоит принципиальная разница между простыми и сложными процентами достаточно просто, но все же нюанс заключается в том, что банки в договоре не указывают такие понятия, как простые и сложные проценты каждый потенциальный вкладчик должен обращать внимание на все условия договора. Если в договоре указано, что проценты выплачиваются по окончании срока действия договора, соответственно, капитализация по такому договору не предусмотрена

Простые проценты

На практике применяются три варианта расчета простых процентов:

точные проценты с точным числом дней ссуды (английская практика). Обозначается как 365/365 или АТС/АТС.
обыкновенные (коммерческие) проценты с точным числом дней ссуды (французская практика). Обозначается как 365/360 или АТС/360.
обыкновенные проценты с приближенным числом дней ссуды (германская практика). Обозначается как 360/360.
По схеме 360 количество дней к году принимается равным 360 (в каждом месяце по 30 дней).
Пример. Определить приближённое число дней между 12.02.2019 и 27.08.2020.
Если год рассматривается как промежуток, содержащий 12 месяцев продолжительностью 30 дней (дивизор равен 360 дней), то приближённое число дней рассчитывается следующим образом:
где y — номер года, m — номер месяца в году, d — номер дня в месяце.
n = 360*(2020-2019)+30*(8-2)+(27-12) = 555 дней

Pin

Когда срок финансовой сделки не равен целому числу лет:
S=P·(1+tT·i)
где t — срок в днях, T — временная база (365 или 360)

Примеры задач на простые проценты

Решить

Ссуда в размере P = 1 млн.руб. выдана d1 = 20.01 до d2 = 05.10 включительно под i = 18% годовых. Какую сумму должен заплатить должник в конце срока при начислении простых процентов? При решении применить три метода расчёта срока ссуды.
Начальная дата: 20.01, конечная дата: 05.10, количество дней между датами: 258
Январь, 11 дней: с 21.01 по 31.01
Февраль, 28 дней: с 01.02 по 28.02
Март, 31 день: с 01.03 по 31.03
Апрель, 30 дней: с 01.04 по 30.04
Май, 31 день: с 01.05 по 31.05
Июнь, 30 дней: с 01.06 по 30.06
Июль, 31 день: с 01.07 по 31.07
Август, 31 день: с 01.08 по 31.08
Сентябрь, 30 дней: с 01.09 по 30.09
Октябрь, 5 дней: с 01.10 по 05.10
Итого: 11 + 28 + 31 + 30 + 31 + 30 + 31 + 31 + 30 + 5 = 258
S=P·(1+tT·i)
1) Точные проценты с точным числом дней ссуды (365/365)
S=1 000 000·(1+258365·0.18)=1 127 232.88 руб.
2) Обыкновенные проценты с точным числом дней (365/360)
S=1 000 000·(1+258360·0.18)=1 129 000 руб.
3) Обыкновенные проценты с приближённым числом дней (360/360)
Количество дней между датами: 255
Январь, 10 дней: с 21.01 по 30.01
Февраль, Март, Апрель, Май, Июнь, Июль, Август, Сентябрь по 30 дней
Октябрь, 5 дней: с 01.10 по 05.10
Итого: 10 + 30*8 + 5 = 255
S=1 000 000·(1+255360·0.18)=1 127 500 руб.
Через d = 180 дней после подписания договора должник уплатит S = 310 тыс.руб. Кредит выдан под i = 16% годовых. Какова первоначальная сумма долга при условии, что временная база равна 365 дням?
P=S(1+tT·i)
Находим современную стоимость P=310 000(1+180365·0.16) = 287 328.59 руб.

Как рассчитать сложный процент по вкладу в банке

Я веду этот блог уже более 6 лет. Все это время я регулярно публикую отчеты о результатах моих инвестиций. Сейчас публичный инвестпортфель составляет более 1 000 000 рублей.

Подробнее

Прежде чем понять, как рассчитать сложный процент по вкладу, давайте разберемся с простыми процентами. Простые проценты часто используют при подсчете прибыли по банковскому депозиту, со снятием дохода в расчетные периоды. К примеру, если мы инвестируем 100$ на 10 лет под 10% годовых, то через год мы сможем забрать всего 110$. А после окончания срока депозита, вклад удвоится.

1-й год: 100$ + 100$*0,10 = 110$ 10-й год: 100 + 100$*0,10*10 лет = 200$

Ощутимым преимуществом простых процентов (инвестирования без капитализации), является возможность использование текущей прибыли в других целях.

Теперь на этом же простом примере разберем, как просчитать сложный процент при ежегодной капитализации.

1-й год: 100 + 10% = 110$ 2-й год: 110 + 10% = 121$ 10-й-год: 236 + 10% = 260$

Как видно из примера, сложный банковский процент существенно интереснее, с применением этого метода прибыль вкладчика на 30% больше, чем при простом проценте. Эта сумма может быть еще большей, если применять не ежегодную капитализацию (начисление процентов), а ежеквартальную или ежемесячную.

Суть процесса начисления сложных процентов с капитализацией в том, что доход приносит не только первоначальная сумма вклада, но и каждое начисление прибыли. При этом сумма увеличивается с большой скоростью, и чем чаще будет фиксироваться прибыль, тем больше будет доход.