Средние величины и показатели вариации

Средневзвешенное значение: особенности

Однако все вышеперечисленные величины могут быть использованы не везде. Например, в статистике при расчете некоторых средних значений важную роль имеет «вес» каждого числа, используемого в вычислениях. Результаты являются более показательными и корректными, поскольку учитывают больше информации. Эта группа величин носит общее название «средневзвешенное значение». Их в школе не проходят, поэтому на них стоит остановиться поподробнее.

Прежде всего, стоит рассказать, что подразумевается под «весом» того или иного значения. Проще всего объяснить это на конкретном примере. Два раза в день в больнице происходит замер температуры тела у каждого пациента. Из 100 больных в разных отделениях госпиталя у 44 будет нормальная температура — 36,6 градусов. У еще 30 будет повышенное значение — 37,2, у 14 — 38, у 7 — 38,5, у 3 — 39, и у двух оставшихся — 40. И если брать среднее арифметическое, то эта величина в общем по больнице будет составлять больше 38 градусов! А ведь почти у половины пациентов совершенно нормальная температура. И здесь корректнее будет использовать средневзвешенное значение, а «весом» каждой величины будет количество людей. В этом случае результатом расчета будет 37,25 градусов. Разница очевидна.

В случае средневзвешенных расчетов за «вес» может быть принято количество отгрузок, число работающих в тот или иной день людей, в общем, все что угодно, что может быть измерено и повлиять на конечный результат.

Какие способы вычисления среднего бывают?

Первым способом является вычисление уже упомянутого среднего арифметического, являющегося суммой всех значений, деленной на их количество.

Формула:

• x– среднее арифметическое;
• x_n – конкретное значение;
• n – количество значений.

Плюсы:

• Хорошо работает при нормальном распределении значений в выборке;
• Легко вычислить;
• Интуитивно понятно.

Минусы:

• Не дает реального представления о распределении значений;
• Неустойчивая величина легко поддающаяся выбросам (как в случае с генеральным директором).

Вторым способом является вычисление моды, то есть наиболее часто встречающегося значения.

Формула:

• M– мода;
• x– нижняя граница интервала, который содержит моду;
• n – величина интервала;
• f_m– частота (сколько раз в ряду встречается то или иное значение);
• f_m-1 – частота интервала предшествующего модальному;
• f_m+1 – частота интервала следующего за модальным.

Плюсы:

• Прекрасно подходит для получения представления об общественном мнении;
• Хорошо подходит для нечисловых данных (цвета сезона, хиты продаж, рейтинги);
• Проста для понимания.

Минусы:

• Моды может просто не быть (нет повторов);
• Мод может быть несколько (многомодальное распределение).

Третий способ — это вычисление медианы, то есть значения, которое делит упорядоченную выборку на две половины и находится между ними. А если такого значения нет, то за медиану принимается среднее арифметическое между границами половин выборки.

Формула:

• M_e – медиана;
• x– нижняя граница интервала, который содержит медиану;
• h – величина интервала;
• f _i – частота (сколько раз в ряду встречается то или иное значение);
• S_m-1 – сумма частот интервалов предшествующих медианному;
• f_m – число значений в медианном интервале (его частота).

Плюсы:

• Дает самую реалистичную и репрезентативную оценку;
• Устойчива к выбросам.

Минусы:

Сложнее вычислить, так как перед вычислением выборку нужно упорядочить.

Мы рассмотрели основные методы нахождения среднего значения, называющиеся мерами центральной тенденции (на самом деле их больше, но это наиболее популярные).

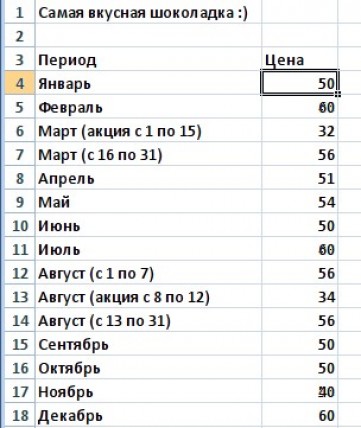
А теперь давайте вернемся к нашему примеру и посчитаем все три варианта среднего при помощи специальных функций Excel:

•  — функция для определения среднего арифметического;
•  — функция моды (в более старых версиях Excel использовалась );
•  — функция для поиска медианы.

И вот какие значения у нас получились:

В данном случае мода и медиана гораздо лучше характеризуют среднюю зарплату в компании.

Но что делать, когда в выборке не 10 значений, как в примере, а миллионы? В Excel это не посчитать, а вот в базе данных где хранятся ваши данные, без проблем.

Вычисляем среднее арифметическое на SQL

Тут все достаточно просто, так как в SQL предусмотрена специальная агрегатная функция .

И чтобы ее использовать достаточно написать вот такой запрос:

/* Здесь и далее salary - столбец с зарплатами, а employees - таблица сотрудников в нашей базе данных */

SELECT AVG(salary) AS 'Средняя зарплата'
FROM employees

Вычисляем моду на SQL

В SQL нет отдельной функции для нахождения моды, но ее легко и быстро можно написать самостоятельно. Для этого нам необходимо узнать, какая из зарплат чаще всего повторяется и выбрать наиболее популярную.

Напишем запрос:

/* WITH TIES необходимо добавлять к TOP() если множество многомодально, то есть у множества несколько мод */
SELECT TOP(1) WITH TIES salary AS 'Мода зарплаты'
FROM employees
GROUP BY salary
ORDER BY COUNT(*) DESC

Вычисляем медиану на SQL

Как и в случае с модой, в SQL нет встроенной функции для вычисления медианы, зато есть универсальная функция для вычисления процентилей .

Выглядит все это так:

/* В данном случае процентиль 0.5 и будет являться медианой */

SELECT TOP(1) PERCENTILE_CONT(0.5)
       WITHIN GROUP (ORDER BY salary)
       OVER() AS 'Медианная зарплата'
FROM employees

Подробнее о работе функции  лучше почитать в справке Microsoft и .

Среднее квадратичное отклонение

Обычно для того, чтобы вычислить усредненное квадратичное отклонение требуется достаточно непростые вычисления. Но в Excel есть готовая формула для получения конечного результата (функция СТАНДОТКЛОН).

Данный показатель привязывается к масштабу исходного значению. Чтобы получить относительный уровень разброса требуется рассчитать коэффициент вариации. Для этого достаточно разделить среднеквадратическое отклонение на усредненное арифметическое

Также стоит учитывать и то, что коэффициент рассчитывается в процентах. Именно поэтому стоит установить формат процентный, а не просто числовой для отображения данных в ячейках.

Подсчёт среднего арифметического пяти

Выполнение данной операции потребует проведения определённого алгоритма действий.

1. Прежде всего, надо выбрать пять чисел, для которых будет проходить вычисление среднего арифметического. После данного подбора эти числа, как и в предыдущих вариантах, необходимо просто сложить и получить конечную сумму.
2. Полученную сумму надо будет поделить по их количеству на пять, что и позволит получить требуемое значение.

Формула

Тем самым аналогично с ранее рассмотренными вариантами получаем такую формулу для подсчёта среднего арифметического:

В данной формуле переменные имеют такое обозначение:

А, В, С, Е и Р – это числа, для которых необходимо получить среднее арифметическое.

Функция СРЗНАЧ.

СРЗНАЧ применяется для возврата среднего арифметического указанных ячеек.

Число 1, 2 и так далее – числа, для которых вы хотите найти среднее. Первый аргумент обязателен, последующие – нет. В одну формулу может быть включено до 255 аргументов. Они могут быть представлены в виде чисел, ссылок на ячейки или диапазонов.

Использование функции СРЗНАЧ – на примерах.

СРЗНАЧ – одна из самых простых и простых в использовании функций Excel, и следующие примеры подтверждают это.

Пример 1. Расчет среднего из нескольких чисел.

Вы можете указать числа непосредственно. Например,

 =СРЗНАЧ(1;2;3;4) возвращает результат 2,5.

Чтобы вычислить среднее по столбцу, укажите ссылку на него целиком:=СРЗНАЧ(A:A)

Чтобы получить  по строке, введите ссылку на нее:=СРЗНАЧ(1:1)

Чтобы вычислить в каком-то диапазоне, укажите его:=СРЗНАЧ(A1:C20)

Чтобы вернуть среднее из несмежных ячеек, запишите каждую ячейку отдельно, например=СРЗНАЧ(A1; C1; D1)

И, естественно, ничто не мешает вам включать числа, ссылки и диапазоны в одну формулу. Например, следующее выражение вычисляет среднее из 2 диапазонов и 1 отдельного значения:

=СРЗНАЧ(B3:B5; C7:D9; B11)

Примечание. Если вы хотите округлить полученное число до ближайшего целого, примените одну из функций округления, например:

Помимо чисел, вы можете использовать функцию СРЗНАЧ для вычисления среднего на основе других видов чисел, таких как проценты и время. Это показано в следующих примерах.

Пример 2. Расчет среднего процента.

Если у вас есть столбец с процентами на вашем листе, как вы получаете средний процент выполнения? Возьмём обычную формулу Excel для среднего 🙂

Примечание. Обратите внимание, что СРЗНАЧ учитывает и нулевые значения при расчете. А это существенно повлияет на итоговую цифру. Если вы предпочитаете исключать нули из расчета, возьмите вместо этого СРЗНАЧЕСЛИ, как будет показано чуть ниже

ССЫЛКА

Пример 3. Расчет среднего времени.

Этим совсем не так просто, как с обычными числами. Ведь время включает часы, минуты и секунды? Вычислять разные единицы времени вручную было бы очень сложно… но СРЗНАЧ отлично с этим справляется.

Важные особенности СРЗНАЧ!

Как вы только что видели, применять СРЗНАЧ очень просто. Тем не менее, у нее есть несколько особенностей, о которых вам нужно знать.

• Нулевые значения (0) включены в расчет.
• Текстовые строки, логические значения ИСТИНА и ЛОЖЬ, а также пустые ячейки — игнорируются. Если вы хотите включить в расчет логические и текстовые представления чисел, примените  СРЗНАЧА.
• Учитываются логические значения, которые вы вводите непосредственно в выражение. Например, =СРЗНАЧ(ИСТИНА; ЛОЖЬ) возвращает 0,5, что является средним из 1 и 0.

Примечание. При использовании СРЗНАЧ в листах Excel, учитывайте различие между ячейками, содержащими нулевые значения, и реально пустыми

Нули считаются, а пустые – нет. Это может быть особенно важно, если опция «Показывать ноль в ячейках, которые содержат нулевые значения» не включена на данном листе. То есть, клетки с нулями внешне будут пустыми. Вы можете найти эту опцию в Эксель: Параметры  > Дополнительно > Параметры отображения листа 

Как найти среднее значение в Excel?

Итак, как обычно рассчитывается среднее арифметическое? Для этого нужно сложить все числа и разделить на их общее количество. Для решения очень простых задач этого достаточно, но во всех остальных случаях такой вариант не подойдет. Дело в том, что в реальной ситуации числа всегда меняются, количество этих чисел тоже. К примеру, у пользователя есть таблица, где указаны оценки студентов. И нужно найти средний балл каждого студента. Понятно, что у каждого из них будут разные оценки, а количество предметов на разных специальностях и на разных курсах тоже будет разным. Было бы очень глупо (и нерационально) все это отслеживать и считать вручную. Да и делать это не понадобится, поскольку в Excel есть специальная функция, которая поможет найти среднее значение любых чисел. Даже если они будут изменяться время от времени, программа будет автоматически пересчитывать новые значения.

Можно предположить, что у пользователя есть уже созданная таблица с двумя колонками: первый столбец — название предмета, а второй — оценка по этому предмету. И необходимо найти средний балл. Для этого надо с помощью мастера функций прописать формулу для расчета среднего арифметического. Делается это достаточно просто:

1. Необходимо выделить любую ячейку и выбрать в панели меню пункты «Вставка — Функция».
2. Откроется новое окно «Мастер функций», где в поле «Категория» надо указать пункт «Статистические».
3. После этого в поле «Выберите функцию» нужно найти строку «СРЗНАЧ» (весь список отфильтрован по алфавиту, так что никаких проблем с поиском возникнуть не должно).
4. Затем откроется еще одно окно, где необходимо указать диапазон ячеек, для которых будет рассчитываться среднее арифметическое.
5. После нажатия кнопки «ОК» результат будет отображен в выбранной ячейке.

Если теперь, например, изменить какое-то значение по одному из предметов (или вовсе его удалить и оставить поле пустым), то Эксель сразу же пересчитает формулу и выдаст новый результат.

Альтернативные способы расчета среднего значения

Пример использования функции СРЗНАЧ для расчета среднего значения диапазона ячеек

Она находится чуть ниже панели меню и чуть выше от первой строки рабочего листа Эксель. Именно здесь отображаются все написанные формулы в программе. Например, если нажать на ячейку, где уже посчитано среднее значение, то в строке формул можно увидеть примерно следующее: =СРЗНАЧ(B1:B6). А чуть левее находится кнопка «fx», нажав на которую, можно открыть знакомое уже окно для выбора нужной функции.

Также можно прописывать любые формулы и вручную. Для этого нужно в любой выбранной ячейке поставить знак «=», прописать вручную формулу (СРЗНАЧ), открыть скобку, выбрать нужный диапазон ячеек и закрыть скобку. Результат тут же будет отображен.

Вот таким простым способом рассчитывается среднее значение в Microsoft Excel. Аналогичным образом можно считать и среднее арифметическое только для нужных полей, а не для всего диапазона ячеек. Для этого во время выбора диапазона ячеек потребуется лишь зажать клавишу «Ctrl» и поочередно щелкать по каждому нужному полю.

Подсчет среднего арифметического

Формула для вычислений предельно проста:

P = (a1 + a2 + … an) / n,

где an – значение величины, n – общее количество значений.

Для чего может использоваться данный показатель? Первое и очевидное его применение — это статистика. Практически в каждом статистическом исследовании используется показатель среднего арифметического. Это может быть средний возраст вступления в брак в России, средняя оценка по предмету у школьника или средние траты на продукты в день. Как уже говорилось выше, без учета весов подсчет средних значений может давать странные или абсурдные значения.

К примеру, президент Российской Федерации сделал заявление, что по статистике, средняя зарплата россиянина составляет 27 000 рублей. Для большинства жителей России такой уровень зарплаты показался абсурдным. Не мудрено, если при расчете учитывать размер доходов олигархов, руководителей промышленных предприятий, крупных банкиров с одной стороны и зарплаты учителей, уборщиков и продавцов с другой. Даже средние зарплаты по одной специальности, например, бухгалтера, будут иметь серьезные отличия в Москве, Костроме и Екатеринбурге.

Физический смысл средней арифметической

Представим, что имеется спица, на которой в разных местах нанизаны грузики различной массы.

Как отыскать центр тяжести? Центр тяжести – это такая точка, за которую можно ухватиться, и спица при этом останется в горизонтальном положении и не будет переворачиваться под действием силы тяжести. Она должна быть в центре всех масс, чтобы силы слева равнялись силам справа. Для нахождения точки равновесия следует рассчитать среднее арифметическое взвешенное расстояний от начала спицы до каждого грузика. Весами будут являться массы грузиков (m_i), что в прямом смысле слова соответствует понятию веса. Таким образом, среднее арифметическое расстояние – это центр равновесия системы, когда силы с одной стороны точки уравновешивают силы с другой стороны.

И последнее. В русском языке так сложилось, что под словом «средний» обычно понимают именно среднее арифметическое. То есть моду и медиану как-то не принято называть средним значением. А вот на английском языке слово «средний» (average) может трактоваться и как среднее арифметическое (mean), и как мода (mode), и как медиана (median). Так что при чтении иностранной литературы следует быть бдительным.

Вычисление среднего арифметического с помощью Мастера функций

Мастер функций – это универсальная возможность Excel, позволяющая осуществлять самые сложные расчеты, при этом не зная названий формул. Достаточно просто выбрать правильную из списка, а потом вести правильные аргументы. Причем все они показываются в отдельном диалоговом окне с подсказками. Так что пользователь легко может разобраться, какая функция за что отвечает и какой она имеет синтаксис.

Чтобы вызвать мастер функций, необходимо нажать комбинацию клавиш Shift + F3 или найти возле строки ввода формул клавишу fx. После того, как это сделать, появится окошко, в котором нам нужно найти функцию «СРЗНАЧ». Значительно проще искать нужную нам функцию, если выбрать ее тип. В специальном выпадающем меню, расположенном в верхней части экрана, нужно выбрать пункт: «Статистические». Тогда перечень существенно сузится и будет проще выбирать.

Потом появится еще одно окно, в котором можно осуществить ввод аргументов функции СРЗНАЧ.

Частный вариант – вызов функции вывода среднего арифметического из ленты. Для этого надо найти вкладку «Формулы», потом перейти в раздел «Другие функции», там навести мышью на пункт «Статистические». После всех этих операций появится функция СРЗНАЧ.

4

Панель формул

Каждый документ содержит панель формул, которая меняется в зависимости от того, какую ячейку выбрать. Если формула там есть, то она там будет записана. Если формула отсутствует, то там тогда будет отображаться просто значение ячейки (например, если там записан просто текст). На этом скриншоте видно конкретный пример, как может использоваться строка ввода формул. С ее помощью можно посмотреть на то, какая формула кроется за определенным числом (13,2) на примере, а также отредактировать аргументы. Или вообще убрать старую формулу и ввести новую. Или убрать все формулы, а оставить пустое значение или число. Возможностей у нее много достаточно. Можно выбрать любую, которая поможет выполнить поставленную задачу.

Ручной ввод функций

Функция СРЗНАЧ относится к простым. Ее легко запомнить, а также она содержит всего один аргумент. Поэтому мы ее введем вручную. В качестве примера будем использовать скриншот, приведенный выше. Как видим, можно использовать два разрозненных диапазона, не соединенных непосредственно между собой. 

Мы введем ее вручную.

=СРЗНАЧ(A1:B1;F1:H1)

Очевидно, что в соответствующих местах нужно выставлять свои адреса. Если нужно, чтобы при копировании в другие ячейки они сохранялись, не стоит забывать делать ссылки абсолютными. Для этого их нужно выделять, а потом нажимать кнопку F4.

Настоятельно рекомендуется запоминать все функции, которые изучаете, потому что в будущем это позволит очень сильно сэкономить время. 

Расчет среднего значения по условию

Может понадобиться находить среднее значение для определенных чисел только при условии, что они соответствуют конкретному критерию. Условие может быть любым, как текстовым, так и числовым. Также она может записываться как непосредственно в формулу, так и в другие ячейки.

Можно, конечно, использовать функцию ЕСЛИ в сочетании с функцией СРЗНАЧ, но это немного тяжеловатая задача. Если приходится эту комбинацию использовать очень часто, на это всё требуется много времени. Значительно разумнее использовать функцию СРЗНАЧЕСЛИ. В ней в разных ситуациях используется два или три аргумента, но их водить всё равно быстрее, чем прописывать две разные функции в одну формулу.

Представим такую ситуацию: нам руководство поставило задачу определить среднее арифметическое для тех значений, которые равняются или больше 10. 

Конечная формула будет следующей:

 =СРЗНАЧЕСЛИ(A1:A8;”>=10″)

5

В результате, получится такое значение.

6

Разберем аргументы этой функции более подробно.

1. Диапазон. Это непосредственно тот диапазон, в котором будет содержаться набор критериев.
2. Условие. Это непосредственно условие. То есть, значение должно как-то соотноситься с критерием. В нашем случае оно должно быть больше или равно 10.
3. Диапазон усреднения. Необязательный аргумент, который используется если значения, для которых нужно искать среднее арифметическое, находятся в другом месте, а не непосредственно являются критериями. 

Мы опустили третий пункт, потому что в первом аргументе диапазон числовой, в то время как его лучше использовать лишь при текстовых критериях там.

Подсчет среднего арифметического

Формула для вычислений предельно проста:

P = (a1 + a2 + … an) / n,

где an – значение величины, n – общее количество значений.

Для чего может использоваться данный показатель? Первое и очевидное его применение — это статистика. Практически в каждом статистическом исследовании используется показатель среднего арифметического. Это может быть средний возраст вступления в брак в России, средняя оценка по предмету у школьника или средние траты на продукты в день. Как уже говорилось выше, без учета весов подсчет средних значений может давать странные или абсурдные значения.

К примеру, президент Российской Федерации сделал заявление, что по статистике, средняя зарплата россиянина составляет 27 000 рублей. Для большинства жителей России такой уровень зарплаты показался абсурдным. Не мудрено, если при расчете учитывать размер доходов олигархов, руководителей промышленных предприятий, крупных банкиров с одной стороны и зарплаты учителей, уборщиков и продавцов с другой. Даже средние зарплаты по одной специальности, например, бухгалтера, будут иметь серьезные отличия в Москве, Костроме и Екатеринбурге.

Смысл коэффициента

Среднее арифметическое — элементарный показатель для сравнения данных и подсчета приемлемого значения. К примеру, в разных магазинах продается банка пива конкретного производителя. Но в одном магазине она стоит 67 рублей, в другом — 70 рублей, в третьем — 65 рублей, а в последнем — 62 рубля. Довольно большой разбег цен, поэтому покупателю будет интересна средняя стоимость банки, чтобы при покупке товара он мог сравнить свои расходы. В среднем банка пива по городу имеет цену:

Средняя цена = (67 + 70 + 65 + 62) / 4 = 66 рублей.

Зная среднюю цену, легко определить где выгодно покупать товар, а где придется переплатить.

Среднее арифметические постоянно используется в статистических расчетах в случаях, если анализируется однородный набор данных. В примере выше — это цена банки пива одной марки. Однако мы не можем сравнить цену на пиво разных производителей или цены на пиво и лимонад, так как в этом случае разброс значений будет больше, средняя цена будет смазана и недостоверна, а сам смысл расчетов исказится до карикатурного «средняя температура по больнице». Для расчета разнородных массивов данных используется среднее арифметическое взвешенное, когда каждое значение получает свой весовой коэффициент.

Вычисление среднего арифметического четырёх

Как уже видно по аналогии с предыдущими вариантами вычисление данного значения для количества, равного четырём, будет носить следующий порядок:

1. Выбираются четыре цифры, для которых надо вычислить среднее арифметическое значение. Далее производится суммирование и нахождение конечного результата этой процедуры.
2. Теперь чтобы получить окончательный результат, следует взять полученную сумму четырёх и разделить её на четыре. Полученные данные и будут требуемым значением.

Формула

Из описанной выше последовательности действий по нахождению среднего арифметического для четырёх, можно получить следующую формулу:

В данной формуле переменные имеют следующее значение:

А, В, С и Е – это те, к которым необходимо найти значение среднего арифметического.

Применяя данную формулу, всегда можно будет вычислять требуемое значение для данного количества чисел.

Шаги

Метод 1 из 4:

Данные

1. 1

   Запишите числовые значения, которые вы собираетесь анализировать.

   Например, 5 школьникам был предложен письменный тест. Их результаты (в баллах по 100 бальной системе): 12, 55, 74, 79 и 90 баллов.

   Мы проанализируем случайно подобранные числовые значения в качестве примера.

Метод 2 из 4:

Среднее значение

1. 1

   Для того чтобы посчитать среднее значение, нужно сложить все имеющиеся числовые значения и разделить получившееся число на их количество.

   • Среднее значение (μ) = Σ/N, где Σ сумма всех числовых значений, а N количество значений.
   • То есть, в нашем случае μ равно (12+55+74+79+90)/5 = 62.

Метод 3 из 4:

Среднее квадратичное отклонение

1

Мы будем считать среднее отклонение.Для вышеуказанного примера это квадратный корень из [((12-62)^2 + (55-62)^2 + (74-62)^2 + (79-62)^2 + (90-62)^2)/(5)] = 27,4

(Обратите внимание, что если это выборочное среднеквадратическое отклонение, то делить нужно на N-1, где N количество значений.)
Среднее отклонение = σ = квадратный корень из [(Σ((X-μ)^2))/(N)]

Метод 4 из 4:

Средняя погрешность среднего значения

1. 1

   Считаем среднюю погрешность (среднего значения).

   Если в нашем примере 5 школьников, а всего в классе 50 школьников, и среднее отклонение, посчитанное для 50 школьников равно 17 (σ = 21), средняя погрешность = 17/кв. корень(5) = 7.6.

   Это оценка того, насколько сильно округляется общее среднее значение. Чем больше числовых значений, тем меньше средняя погрешность, тем точнее среднее значение. Для расчета погрешности надо разделить среднее отклонение на корень квадратный от N. Стандартная погрешность = σ/кв.корень(n).

Советы

• Расчеты среднего значения, среднего отклонения и погрешности годятся для анализа равномерно распределенных данных. Среднее отклонение математического среднего значения распределения относится приблизительно к 68% данных, 2 средних отклонения – к 95% данных, а 3 – к 99.7% данных. Стандартная погрешность же уменьшается при увеличении количества значений.
• Простой в использовании калькулятор для расчета среднего отклонения.