Basic math in javascript

Содержание:

Сравнение чисел
- Основные математические операции
Интересный факт о strictfp
Rounding the Number
- Rounding to the Nearest Integer
- Rounding to Arbitrary Levels of Precision
Неточные вычисления
Сравнение чисел
- Основные математические операции
Set functions #
Устройство чисел с плавающей точкой
Why Round Numbers?
Великий и могучий Math
Сравнение дробных чисел
JavaScript
Комментарии
Floor(Double)
Как явно преобразовать строку в число?
Функция isFinite
Целая и дробная часть числа
- Делится ли число нацело
Как явно преобразовать строку в число
Округление чисел в JavaScript (floor, ceil, round, trunc, toFixed)
- Встроенные функции JavaScript для округления чисел до целого:
- Метод JavaScript toFixed(m) для округления чисел до заданной точности:

Сравнение чисел

Для сравнения чисел в JavaScript используются следующие операторы: == (равно), != (не равно), > (больше), = (больше или равно),

Например, сравним два числа:

Console.log(2>3); //false
console.log(5>=3); //true

При сравнении чисел с дробной частью необходимо учитывать погрешности, которые могут возникать во время этих вычислений.

Например, в JavaScript сумма чисел (0.2 + 0.4) не равна 0.6:

Console.log((0.2+0.4)==0.6); //false

Погрешности происходят потому что все вычисления компьютер или другое электронное устройство производит в 2 системе счисления. Т.е. перед тем как выполнить какие-то действия компьютер сначала должен преобразовать представленные в выражении числа в 2 систему счисления. Но, не любое дробное десятичное число можно представить в 2 системе счисления точно.

Например, число 0.25 10 в двоичную систему преобразуется точно.

0.125 × 2 = 0.25 | 0
0.25 × 2 = 0.5 | 0
0.5 × 2 = 1 | 1
0.125 10 = 0.001 2

Например, число 0.2 10 можно преобразовать в 2 систему только с определённой точностью:

0.2 × 2 = 0.4 | 0
0.4 × 2 = 0.8 | 0
0.8 × 2 = 1.6 | 1
0.6 × 2 = 1.2 | 1
0.2 × 2 = 0.4 | 0
0.4 × 2 = 0.8 | 0
0.8 × 2 = 1.6 | 1
0.6 × 2 = 1.2 | 1
0.2 × 2 = 0.4 | 0
0.4 × 2 = 0.8 | 0
0.8 × 2 = 1.6 | 1
0.6 × 2 = 1.2 | 1
…
0.2 10 = 0.001100110011… 2

В результате эти погрешности скажутся при вычисления суммы двух чисел и результатах сравнения. Т.е. получится что на самом деле JavaScript будет видет эту запись следующим образом:

0.6000000000000001==0.6

При вычислениях или отображении чисел с дробной частью необходимо всегда указывать точность, с которой это необходимо делать.

Например, сравнить числа до 2 знаков после запятой используя методы toFixed() и toPrecision() :

//метод toFixed()
console.log((0.2+0.4).toFixed(2)==(0.6).toFixed(2)); //true
//метод toPrecision()
console.log((0.2+0.4).toPrecision(2)==(0.6).toPrecision(2)); //true

Основные математические операции

В JavaScript существуют следующие математические операторы: + (сложение), — (вычитание), * (умножение), / (деление), % (остаток от деления), ++ (увелить значение на 1), — (уменьшить значение на 1).

6+3 //9
6-3 //3
6*3 //18
6/3 //2
6%3 //0, т.е. 6:3=2 => 6-3*2 => ост(0)
5%2 //1, т.е. 5:2=2(.5) => 5-2*2 => ост(1)
7.3%2 //1.3, т.е. 7.3:2=3(.65) => 7.3-2*3 => ост(1.3)
//знак результата операции % равен знаку первого значения
-9%2.5 //-1.5, т.е. 9:2.5=3(.6) => 9-2.5*3 => ост(1.5)
-9%-2.5 //-1.5, т.е. 9:2.5=3(.6) => 9-2.5*3 => ост(1.5)
-2%5 //-2, т.е. 2:5=0(.4) => 2-5*0 => ост(2)
x = 3;
console.log(x++); //выводит 3, у уже потом устанавливает 4
console.log(x); //4
x = 3;
console.log(++x); //устанавливает 4 и выводит
x = 5;
console.log(x—); //выводит 5, у уже потом устанавливает 4
console.log(x); //4
x = 5;
console.log(—x); //устанавливает 4 и выводит
Кроме этого в JavaScript есть комбинированные операторы: x+=y (x=x+y), x-=y (x=x-y), x*=y (x=x*y), x/=y (x=x/y), x%=y (x=x%y).
x = 3;
y = 6;
x+=y;
console.log(x); //9
x = 3;
y = 6;
x-=y;
console.log(x); //-3
x = 3;
y = 6;
x*=y;
console.log(x); //18
x = 3;
y = 6;
x/=y;
console.log(x); //0.5
x = 3;
y = 6;
x%=y;
console.log(x); //3

Здравствуйте, любители JavaScript-а. Вы уже заметили, что этот язык очень неординарен и в каждом разделе выделяется своими особенностями и необычными техническими решениями. Поэтому сегодняшняя публикация посвящается теме: «JavaScript округление».

После прочтения текущей статьи вы узнаете, для чего необходимо округлять числа, какие методы и свойства в js выполняют эту функцию, а также чем выделяется деление на 0. Не изменяя своим принципам, я прикреплю примеры к ключевым моментам материала и подробно распишу каждое действие. А теперь давайте приступать к обучению!

Интересный факт о strictfp

В Java есть специальное ключевое слово (strict floating point), которого нет в других языках программирования. И знаете, зачем оно нужно? Оно ухудшает точность работы с вещественными числами. История его появления примерно такова:

Создатели Java:

Мы очень хотим, чтобы Java была суперпопулярна, и программы на Java выполнялись на как можно большем количестве устройств. Поэтому мы прописали в спецификацию Java-машины, что на всех типах устройств все программы должны выполняться одинаково!

Создатели процессора Intel:

Ребята, мы улучшили наши процессоры, и теперь все вещественные числа внутри процессора будет представлены не 8-ю, а 10-ю байтами. Больше байт — больше знаковых цифр. А это значит что? Правильно: теперь ваши научные вычисления будут еще более точными!

Ученые и все, кто занимается сверхточными расчетами:

Круто! Молодцы. Отличная новость.

Создатели Java:

Не-не-не, ребята. Мы же сказали: все Java-программы должны выполняться одинаково на всех устройствах. Принудительно выключаем возможность использования 10 байтовых вещественных чисел внутри процессоров Intel.

Вот теперь все опять отлично! Не благодарите.

Ученые и все, кто занимается сверхточными расчетами:

Да вы там совсем охренели? Ану быстро вернули все как было!

Создатели Java:

Ребята, это для вашей же пользы! Только представьте: все Java-программы выполняются одинаково на всех устройствах. Ну круто же!

Ученые и все, кто занимается сверхточными расчетами:

Нет. Совсем не круто. Быстро вернули все обратно! Или мы вашу Java вам знаете куда засунем?

Создатели Java:

Гм. Что же вы сразу не сказали. Конечно, вернем.

Вернули возможность пользоваться всеми фичами крутых процессоров.

Кстати. Мы так же специально добавили в язык слово : если его написать перед именем функции, вся работа с вещественными числами внутри этой функции будет одинаково плохой на всех устройствах!

Rounding the Number

Whatever your reason for rounding numbers may be, JavaScript has
several ways of allowing you to round numbers. Let us look at the most
common ones.

Rounding to the Nearest Integer

The most common function for rounding your value is the prom king
himself, Math.round:

Math.round(1.532); // 2
Math.round(1.235); // 1
Math.round(27.94); // 28
Math.round(0.0005); // 0

This function works by rounding your number to the nearest integer.
If the first number after the decimal is 5 or higher, it rounds up. If
the first number after the decimal is 4 or lower, it rounds down. The
Math.round function most closely
resembles what you may have learned in school.

Its equally popular variants are the
Math.floor and
Math.ceil functions. Whereas Math.round
would either round up or down depending on what the number after the
decimal is, Math.floor will always round
down to the next lowest integer regardless of what the value after the
decimal is. Similarly…in an opposite way,
Math.ceil will always round up to the next highest integer
regardless of what the value after the decimal actually is:

Math.ceil(1.5); // 2
Math.floor(1.5); // 1
Math.floor(1.235); // 1
Math.ceil(0.0005); // 1

All of this should look pretty straightforward. Just to drive the point
home about the next highest and lowest integers, let’s look what happens
when we are dealing with negative values:

Math.ceil(-45) // -45
Math.floor(-45) // -45
Math.ceil(-.5) // 0
Math.floor(-.5) // -1
Math.round(-45) // -45
Math.round(-.5) // -1
Math.round(-1.24) // -1

The Math.ceil and
Math.floor functions work as expected.
They round up or down to the next largest or smallest integer. Remember,
in the negative world, the smaller the absolute value of your number,
the larger its actual value:

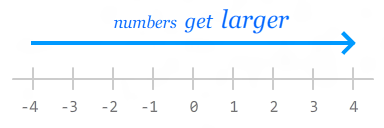
That is why rounding up from -.5
results in you getting . If you think
of the relative size of numbers as being on the number line,
Math.ceil goes right.
Math.floor goes left. It’s like opposite day over there.

Our prom king Math.round, though,
exhibits some slightly shallow behavior. Instead of rounding up or down
to the nearest large or small number, this function literally rounds up or
rounds down based on the absolute value of the number. That is why
rounding -.5 is actually a
-1 (a smaller number) than being 0 like
you may expect.

Rounding to Arbitrary Levels of Precision

In the previous section, you learned how you can round to the nearest
integer. There will be times when you want to round to a particular
decimal position for extra preciseness. Let’s say we want to round our value of Pi to just 2 digits past the
decimal point. In other words, we want 3.14159
to be rounded off to 3.14. Using the
three amigos (Math.round,
Math.floor, and
Math.ceil) without any modification will cause our value to either
be 3 or 4. That’s not what we want.

To get what we want, there is a simple approach we can take made up of just three steps:

To get X digits of precision, multiply our number by 10 to the power of X.
Round the result using Math.round()
Divide the new result by 10 to the power of X again.

To make this more concrete, let’s see we want to round 3.14159 to two digits of precision. To get two decimal positions of precision,
we can multiply our number by 10 to the power of two
(aka 100) and round that value:

Math.round(3.14159 * 100);

Next, divide the result of this rounding
operation by 10 to the power of two again to get
the answer you are looking for:

Math.round(3.14159 * 100) / 100; // result is 3.14

To generalize this a bit, here is a basic formula:

The d stands for the number of places after
the decimal point you want to go to. The number
is the value you are trying to round. Everything else should be
self-explanatory.

Using this model, here is how we can round 3.14159 to the tenths,
hundredths, thousandths, and ten thousandths positions:

Math.round(3.14159 * 10) / 10; // 3.1
Math.round(3.14159 * 100) / 100; // 3.14
Math.round(3.14159 * 1000) / 1000; // 3.142
Math.round(3.14159 * 10000) / 10000; // 3.1416

You can substitute Math.round with
Math.floor or
Math.ceil depending on what exactly you are going for, and the
behavior will be predictable.

Неточные вычисления

Внутри JavaScript число представлено в виде 64-битного формата IEEE-754. Для хранения числа используется 64 бита: 52 из них используется для хранения цифр, 11 из них для хранения положения десятичной точки (если число целое, то хранится 0), и один бит отведён на хранение знака.

Если число слишком большое, оно переполнит 64-битное хранилище, JavaScript вернёт бесконечность:

Наиболее часто встречающаяся ошибка при работе с числами в JavaScript – это потеря точности.

Посмотрите на это (неверное!) сравнение:

Да-да, сумма и не равна .

Странно! Что тогда, если не ?

Но почему это происходит?

Число хранится в памяти в бинарной форме, как последовательность бит – единиц и нулей. Но дроби, такие как , , которые выглядят довольно просто в десятичной системе счисления, на самом деле являются бесконечной дробью в двоичной форме.

Другими словами, что такое ? Это единица делённая на десять — , одна десятая. В десятичной системе счисления такие числа легко представимы, по сравнению с одной третьей: , которая становится бесконечной дробью .

Деление на гарантированно хорошо работает в десятичной системе, но деление на – нет. По той же причине и в двоичной системе счисления, деление на обязательно сработает, а становится бесконечной дробью.

В JavaScript нет возможности для хранения точных значений 0.1 или 0.2, используя двоичную систему, точно также, как нет возможности хранить одну третью в десятичной системе счисления.

Числовой формат IEEE-754 решает эту проблему путём округления до ближайшего возможного числа. Правила округления обычно не позволяют нам увидеть эту «крошечную потерю точности», но она существует.

Пример:

И когда мы суммируем 2 числа, их «неточности» тоже суммируются.

Вот почему – это не совсем .

Не только в JavaScript

Справедливости ради заметим, что ошибка в точности вычислений для чисел с плавающей точкой сохраняется в любом другом языке, где используется формат IEEE 754, включая PHP, Java, C, Perl, Ruby.

Можно ли обойти проблему? Конечно, наиболее надёжный способ — это округлить результат используя метод toFixed(n):

Также можно временно умножить число на 100 (или на большее), чтобы привести его к целому, выполнить математические действия, а после разделить обратно. Суммируя целые числа, мы уменьшаем погрешность, но она все равно появляется при финальном делении:

Таким образом, метод умножения/деления уменьшает погрешность, но полностью её не решает.

Забавный пример

Попробуйте выполнить его:

Причина та же – потеря точности. Из 64 бит, отведённых на число, сами цифры числа занимают до 52 бит, остальные 11 бит хранят позицию десятичной точки и один бит – знак. Так что если 52 бит не хватает на цифры, то при записи пропадут младшие разряды.

Интерпретатор не выдаст ошибку, но в результате получится «не совсем то число», что мы и видим в примере выше. Как говорится: «как смог, так записал».

Два нуля

Другим забавным следствием внутреннего представления чисел является наличие двух нулей: и .

Все потому, что знак представлен отдельным битом, так что, любое число может быть положительным и отрицательным, включая нуль.

В большинстве случаев это поведение незаметно, так как операторы в JavaScript воспринимают их одинаковыми.

Сравнение чисел

Для сравнения чисел в JavaScript используются следующие операторы: (равно), (не равно), (больше), (меньше), (больше или равно), (меньше или равно).

Например, сравним два числа:

console.log(2>3); //false
console.log(5>=3); //true

Например, в JavaScript сумма чисел (0.2 + 0.4) не равна 0.6:

console.log((0.2+0.4)==0.6); //false

Например, число 0.25₁₀ в двоичную систему преобразуется точно.

0.125 × 2 = 0.25 | 0
0.25 × 2 = 0.5 | 0
0.5 × 2 = 1 | 1

0.125₁₀ = 0.001₂

Например, число 0.2₁₀ можно преобразовать в 2 систему только с определённой точностью:

0.2 × 2 = 0.4 | 0
0.4 × 2 = 0.8 | 0
0.8 × 2 = 1.6 | 1
0.6 × 2 = 1.2 | 1
0.2 × 2 = 0.4 | 0
0.4 × 2 = 0.8 | 0
0.8 × 2 = 1.6 | 1
0.6 × 2 = 1.2 | 1
0.2 × 2 = 0.4 | 0
0.4 × 2 = 0.8 | 0
0.8 × 2 = 1.6 | 1
0.6 × 2 = 1.2 | 1
...

0.2₁₀ = 0.001100110011...₂

0.6000000000000001==0.6

Например, сравнить числа до 2 знаков после запятой используя методы и :

//метод toFixed()
console.log((0.2+0.4).toFixed(2)==(0.6).toFixed(2)); //true
//метод toPrecision()
console.log((0.2+0.4).toPrecision(2)==(0.6).toPrecision(2)); //true

Основные математические операции

В JavaScript существуют следующие математические операторы: (сложение), (вычитание), (умножение), (деление), (остаток от деления), (увелить значение на 1), (уменьшить значение на 1).

6+3 //9
6-3 //3
6*3 //18
6/3 //2
6%3 //0, т.е. 6:3=2 => 6-3*2 => ост(0)
5%2 //1, т.е. 5:2=2(.5) => 5-2*2 => ост(1)
7.3%2 //1.3, т.е. 7.3:2=3(.65) => 7.3-2*3 => ост(1.3)
//знак результата операции % равен знаку первого значения
-9%2.5 //-1.5, т.е. 9:2.5=3(.6) => 9-2.5*3 => ост(1.5)
-9%-2.5 //-1.5, т.е. 9:2.5=3(.6) => 9-2.5*3 => ост(1.5)
-2%5 //-2, т.е. 2:5=0(.4) => 2-5*0 => ост(2)
x = 3;
console.log(x++); //выводит 3, у уже потом устанавливает 4
console.log(x); //4
x = 3;
console.log(++x); //устанавливает 4 и выводит
x = 5;
console.log(x--); //выводит 5, у уже потом устанавливает 4
console.log(x); //4
x = 5;
console.log(--x); //устанавливает 4 и выводит

x = 3;
y = 6;
x+=y;
console.log(x); //9
x = 3;
y = 6;
x-=y;
console.log(x); //-3
x = 3;
y = 6;
x*=y;
console.log(x); //18
x = 3;
y = 6;
x/=y;
console.log(x); //0.5
x = 3;
y = 6;
x%=y;
console.log(x); //3

Set functions #

Function	Description
math.setCartesian(set1, set2)	Create the cartesian product of two (multi)sets.
math.setDifference(set1, set2)	Create the difference of two (multi)sets: every element of set1, that is not the element of set2.
math.setDistinct(set)	Collect the distinct elements of a multiset.
math.setIntersect(set1, set2)	Create the intersection of two (multi)sets.
math.setIsSubset(set1, set2)	Check whether a (multi)set is a subset of another (multi)set.
math.setMultiplicity(element, set)	Count the multiplicity of an element in a multiset.
math.setPowerset(set)	Create the powerset of a (multi)set.
math.setSize(set)	Count the number of elements of a (multi)set.
math.setSymDifference(set1, set2)	Create the symmetric difference of two (multi)sets.
math.setUnion(set1, set2)	Create the union of two (multi)sets.

Устройство чисел с плавающей точкой

Тип может хранить значения в диапазоне до . Такой гигантский диапазон значений (по сравнению с типом ) объясняется тем, что тип (как и ) устроен совсем иначе по сравнению с целыми типами. Каждая переменная типа содержит два числа: первое называется мантисса, а второе — степень.

Допустим, у нас есть число , и мы сохранили его в переменную типа . Тогда число будет преобразовано к виду , и внутри типа будут храниться два числа — и . Красным выделена «значащая часть числа» (манти́сса), синим — степень.

Такой подход позволяет хранить как очень большие числа, так и очень маленькие. Но т.к. размер числа ограничен 8 байтами (64 бита) и часть бит используется под хранение
степени (а также знака числа и знака степени), максимальная длина
мантиссы ограничена 15 цифрами.

Why Round Numbers?

You may be wondering why anybody would want to go from having values
that are more precise to having values that are less precise. In this
section, we are going to look at some examples.

Displaying on the Pixel

Whenever you are doing anything on the canvas or positioning DOM elements using code, you’ll be doing a whole lot of pixel pushing to the screen. The things you are drawing on screen look best when its position and size values fall on a whole pixel. If you are using
fractional values, what you are displaying may end up looking blurry:

An easy way to ensure everything falls on pixel boundaries is to
round any position or size value to a whole number.

Improving Performance

Working with round numbers is faster
than having to deal with numbers that contain extra precision. Nuff said about that 😛

Dealing with JavaScript’s Quirky Number Handling

JavaScript stores all numbers internally as floating point values.
This means your calculations could be subject to floating point
shenanigans. Here is an example:

var blah = 0.2 * 0.4;

What do you think the value of blah actually is? If you guessed .08,
you would be wrong. Here is what actually shows up:

There is a reason why the 2 awkwardly shows up at the end of the result. It has to do with how
fractions are represented as floating point values. It is weird, but
that’s just how it is. By rounding your number, you can account for the unnecessary
precision and just get .08 like you probably wanted all along.

Великий и могучий Math

Глобальный объект Math включает в себя огромное количество разнообразных математических и тригонометрических функций. Это очень нужный объект и часто выручает разработчиков при работе с цифровыми данными.

На других платформах существуют аналогии Math. Например, в таких популярных языках, как Java и C#, Math представляет собой класс, который поддерживает все те же стандартные функции. Так что как видите этот инструмент действительно великий и могучий.

Теперь я хочу пройтись по конкретным методам, отвечающим за округление, и подробно о них рассказать.

Math.floor ()

Начну с Math.
floor

Обратите внимание на наименование метода. Логически становится понятно, что раз речь идет об округлении, а дословный перевод слова «floor» означает «пол», то данный инструмент округлит обрабатываемые значения в меньшую строну

Также возможен вариант, когда обработанное число с помощью этой функции осталось прежним. Все потому, что округление осуществляется по нестрогому неравенству (

в ответе будет число 4.

Math.ceil ()

Опять-таки посмотрите на название (в такой способ материал быстрее усваивается). Если кто-то не знает, то «ceil» означает «потолок». Значит округление числовых данных будет осуществляться в большую сторону, используя нестрогое неравенство (>=).

Как вы уже догадались, в ответе будет число 5.

Math.round ()

Данный метод округляет дробное число до ближайшего целого. Так, если дробная часть находится в диапазоне от 0 и до 0.5 не включительно, то округление происходит к меньшему значению. А если дробная часть находится в диапазоне от включительно 0.5 и до следующего целого числа, то она округляется к большему целому.

Надеюсь, все подумали или сказали правильный ответ – 5.

Сравнение дробных чисел

У математических вычислений есть одна особенность — их результат не всегда абсолютно точный. Это проблема
не только JavaScript, но и большинства языков программирования. Так происходит потому, что числа и другие
данные переводятся в двоичный код, и только потом с ними производятся вычисления. В большинстве случаев это
не приводит к особенным трудностям, просто в результате расчётов иногда получается число с большим количеством
знаков после запятой. Но есть ситуация, когда неточность вычислений влияет на работу программы. Это сравнение
чисел. Если сравниваются разные числа, то здесь всё должно быть нормально.

5.1

Но если при вычислении получаются два одинаковых дробных числа, то результат их сравнения не предсказуем.
Они могут быть равны, либо одно может быть больше другого. Когда в скрипте
используется такое сравнение,
то нужно проверять, правильно ли работает скрипт. Если в нём есть ошибка, то нужно округлять значения, которые
сравниваются.

JavaScript

JS Array
concat()
constructor
copyWithin()
entries()
every()
fill()
filter()
find()
findIndex()
forEach()
from()
includes()
indexOf()
isArray()
join()
keys()
length
lastIndexOf()
map()
pop()
prototype
push()
reduce()
reduceRight()
reverse()
shift()
slice()
some()
sort()
splice()
toString()
unshift()
valueOf()

JS Boolean
constructor
prototype
toString()
valueOf()

JS Classes
constructor()
extends
static
super

JS Date
constructor
getDate()
getDay()
getFullYear()
getHours()
getMilliseconds()
getMinutes()
getMonth()
getSeconds()
getTime()
getTimezoneOffset()
getUTCDate()
getUTCDay()
getUTCFullYear()
getUTCHours()
getUTCMilliseconds()
getUTCMinutes()
getUTCMonth()
getUTCSeconds()
now()
parse()
prototype
setDate()
setFullYear()
setHours()
setMilliseconds()
setMinutes()
setMonth()
setSeconds()
setTime()
setUTCDate()
setUTCFullYear()
setUTCHours()
setUTCMilliseconds()
setUTCMinutes()
setUTCMonth()
setUTCSeconds()
toDateString()
toISOString()
toJSON()
toLocaleDateString()
toLocaleTimeString()
toLocaleString()
toString()
toTimeString()
toUTCString()
UTC()
valueOf()

JS Error
name
message

JS Global
decodeURI()
decodeURIComponent()
encodeURI()
encodeURIComponent()
escape()
eval()
Infinity
isFinite()
isNaN()
NaN
Number()
parseFloat()
parseInt()
String()
undefined
unescape()

JS JSON
parse()
stringify()

JS Math
abs()
acos()
acosh()
asin()
asinh()
atan()
atan2()
atanh()
cbrt()
ceil()
clz32()
cos()
cosh()
E
exp()
expm1()
floor()
fround()
LN2
LN10
log()
log10()
log1p()
log2()
LOG2E
LOG10E
max()
min()
PI
pow()
random()
round()
sign()
sin()
sqrt()
SQRT1_2
SQRT2
tan()
tanh()
trunc()

JS Number
constructor
isFinite()
isInteger()
isNaN()
isSafeInteger()
MAX_VALUE
MIN_VALUE
NEGATIVE_INFINITY
NaN
POSITIVE_INFINITY
prototype
toExponential()
toFixed()
toLocaleString()
toPrecision()
toString()
valueOf()

JS OperatorsJS RegExp
constructor
compile()
exec()
g
global
i
ignoreCase
lastIndex
m
multiline
n+
n*
n?
n{X}
n{X,Y}
n{X,}
n$
^n
?=n
?!n
source
test()
toString()

(x|y)
.
\w
\W
\d
\D
\s
\S
\b
\B
\0
\n
\f
\r
\t
\v
\xxx
\xdd
\uxxxx

JS Statements
break
class
continue
debugger
do…while
for
for…in
for…of
function
if…else
return
switch
throw
try…catch
var
while

JS String
charAt()
charCodeAt()
concat()
constructor
endsWith()
fromCharCode()
includes()
indexOf()
lastIndexOf()
length
localeCompare()
match()
prototype
repeat()
replace()
search()
slice()
split()
startsWith()
substr()
substring()
toLocaleLowerCase()
toLocaleUpperCase()
toLowerCase()
toString()
toUpperCase()
trim()
valueOf()

Floor(Double)

Возвращает наибольшее целое число, которое меньше или равно заданному числу с плавающей запятой двойной точности.Returns the largest integral value less than or equal to the specified double-precision floating-point number.

d: Double

Число двойной точности с плавающей запятой.A double-precision floating-point number.

Возвращаемое значение

Double

Наибольшее целое число, которое меньше или равно .The largest integral value less than or equal to . Если значение параметра равно NaN, NegativeInfinity или PositiveInfinity, возвращается это значение.If is equal to NaN, NegativeInfinity, or PositiveInfinity, that value is returned.

Примеры

В следующем примере показан метод и его отличие от метода.The following example illustrates the method and contrasts it with the method.

Поведение этого метода соответствует стандарту IEEE 754, разделу 4.The behavior of this method follows IEEE Standard 754, section 4. Этот тип округления иногда называют округлением в сторону отрицательной бесконечности.This kind of rounding is sometimes called rounding toward negative infinity. Иными словами, если является положительным, любой дробный компонент усекается.In other words, if is positive, any fractional component is truncated. Если имеет отрицательное значение, присутствие любого компонента дробной части приводит к округлению его до меньшего целого числа.If is negative, the presence of any fractional component causes it to be rounded to the smaller integer. Операция этого метода отличается от Ceiling метода, который поддерживает округление в сторону положительной бесконечности.The operation of this method differs from the Ceiling method, which supports rounding toward positive infinity.

Начиная с Visual Basic 15,8, производительность преобразования типа «двойное в целое число» оптимизирована, если передать значение, возвращаемое методом, в любую функцию целочисленного преобразованияили если значение Double, возвращаемое, автоматически преобразуется в целое число с параметром Option-on , равным OFF.Starting with Visual Basic 15.8, the performance of Double-to-integer conversion is optimized if you pass the value returned by the method to the any of the integral conversion functions, or if the Double value returned by is automatically converted to an integer with Option Strict set to Off. Эта оптимизация позволяет коду выполняться быстрее — до двух раз быстрее для кода, который выполняет большое количество преобразований в целочисленные типы.This optimization allows code to run faster — up to twice as fast for code that does a large number of conversions to integer types. В следующем примере показаны оптимизированные преобразования:The following example illustrates such optimized conversions:

Как явно преобразовать строку в число?

Явно привести строку в число можно посредством следующих способов:

1. Использовать унарный оператор +
, который необходимо поместить перед значением.

+»7.35″; // 7.35
+»текст»; // NaN

Этот способ пренебрегает пробелами в начале и конце строки, а также \n (переводом строки).

+» 7.35 «; //7.35
+»7.35 \n «; //7.35

Используя данный способ необходимо обратить внимание на то, что пустая строка или строка, состоящая из пробелов и \n , переводится в число 0. Кроме этого она также преобразует тип данных null и логические значения к числу

Null; //0
+true; //1
+false; //0
+» «; //0

2. Функция parseInt
. Данная функция предназначена для преобразования аргумента в целое число
. В отличие от использования унарного оператора +
, данный метод позволяет преобразовать строку в число, в которой не все символы являются цифровыми
. Начинает она преобразовывать строку, начиная с первого символа. И как только она встречает символ, не являющийся цифровым, данная функция останавливает свою работу и возвращает полученное число.

ParseInt(«18px»); //18
parseInt(«33.3%»); //33

Данная функция может работать с разными системами счисления (двоичной, восьмеричной, десятичной, шестнадцатеричной). Указание основание системы счисления осуществляется посредством 2 аргумента.

ParseInt(«18px», 10); //18
parseInt(«33.3%», 10); //33
parseInt(«101»,2); //5
parseInt(«B5»,16); //181

Кроме функции parseInt
в JavaScript имеется метод Number.parseInt
. Данный метод ничем не отличается от функции parseInt
и был введён в JavaScript со спецификацией ECMASCRIPT 2015 (6).

3. Функция parseFloat
. Функция parseFloat
аналогична parseInt
, за исключением того что позволяет выполнить преобразование аргумента в дробное число.

ParseFloat(«33.3%»); //33.3

Кроме этого функция parseFloat
в отличие от parseInt
не имеет 2 аргумента, и следовательно она всегда пытается рассмотреть строку как число в десятичной системе счисления.

ParseFloat(«3.14»);
parseFloat(«314e-2»);
parseFloat(«0.0314E+2»);

Кроме функции parseFloat
в JavaScript имеется метод Number.parseFloat
. Данный метод ничем не отличается от функции parseFloat
и был введён в JavaScript со спецификацией ECMASCRIPT 2015 (6).

Функция isFinite

Функция isFinite позволяет проверить, является ли аргумент конечным числом.

В качестве ответа данная функция возвращает , если аргумент является , , или будет быть приведён к одному из этих специальных числовых значений. В противном случае данная функция вернёт значение .

isFinite(73);        // true 
isFinite(-1/0);      // false 
isFinite(Infinity);  // false 
isFinite(NaN);       // false 
isFinite('Текст');   // false

Кроме глобальной функции isFinite в JavaScript имеется ещё метод Number.isFinite. Он в отличие от isFinite не осуществляет принудительное приведения аргумента к числу.

isFinite('73');        // true
Number.isFinite('73'); // false

Целая и дробная часть числа

Получить целую часть числа можно используя метод Math.floor() и parseInt() :

Console.log(Math.floor(7.21)); // 7
console.log(parseInt(7.21)); // 7

Получить дробную часть числа можно воспользовавшимся оператором процент (%). Данный оператор возвращает остаток, который будет получен от деления первого числа на второе. В данном случае в качестве 2 числа необходимо использовать 1.

Console.log(7.21%1); // 0.20999999999999996
// с точностью до 2 знаков после запятой
console.log((7.21%1).toFixed(2)); // «0.21»

Кроме этого дробную часть можно получить также с помощью вычислений:

Var number = 7.21;
var fractionNumber = number — Math.floor(Math.abs(number));
console.log(fractionNumber); // 0.20999999999999996

Делится ли число нацело

Определить делится ли число нацело можно используя оператор процента:

Var number = 9;
// если остаток от деления числа number на 3 равен 0, то да, иначе нет
if (number%3==0) {
console.log («Число » + number + » делится на 3″);
} else {
console.log («Число » + number + » не делится на 3″);
}

Как явно преобразовать строку в число

Явно привести строку в число можно посредством следующих способов:

1. Использовать унарный оператор +, который необходимо поместить перед значением.

+'7.35';   // 7.35
+'текст';  // NaN

Этот способ пренебрегает пробелами в начале и конце строки, а также (переводом строки).

+' 7.35 ';    //7.35
+'7.35 \n ';  //7.35

Используя данный способ необходимо обратить внимание на то, что пустая строка или строка, состоящая из пробелов и , переводится в число 0. Кроме этого она также преобразует тип данных и логические значения к числу

+null;   //0
+true;   //1
+false;  //0
+'   ';  //0

2. Функция parseInt. Данная функция предназначена для преобразования аргумента в целое число. В отличие от использования унарного оператора +, данный метод позволяет преобразовать строку в число, в которой не все символы являются цифровыми. Начинает она преобразовывать строку, начиная с первого символа. И как только она встречает символ, не являющийся цифровым, данная функция останавливает свою работу и возвращает полученное число.

parseInt('18px');   //18
parseInt('33.3%');  //33

Кроме этого рекомендуется, всегда указывать основание системы счисления и не полагаться на значение по умолчанию установленное этой функции, например в том или ином браузере.

parseInt('18px', 10);   //18
parseInt('33.3%', 10);  //33
parseInt('101',2);      //5
parseInt('B5',16);      //181

Кроме функции parseInt в JavaScript имеется метод Number.parseInt. Данный метод ничем не отличается от функции parseInt и был введён в JavaScript со спецификацией ECMASCRIPT 2015 (6).

3. Функция parseFloat. Функция parseFloat аналогична parseInt, за исключением того что позволяет выполнить преобразование аргумента в дробное число.

parseFloat('33.3%');  //33.3

Кроме этого функция parseFloat в отличие от parseInt не имеет 2 аргумента, и следовательно она всегда пытается рассмотреть строку как число в десятичной системе счисления.

parseFloat("3.14");
parseFloat("314e-2");
parseFloat("0.0314E+2");

Кроме функции parseFloat в JavaScript имеется метод Number.parseFloat. Данный метод ничем не отличается от функции parseFloat и был введён в JavaScript со спецификацией ECMASCRIPT 2015 (6).

Округление чисел в JavaScript (floor, ceil, round, trunc, toFixed)

Встроенные функции JavaScript для округления чисел до целого:

Math.floor — округление в меньшую сторону.
Math.ceil — округление в большую сторону.
Math.round — округление до ближайшего целого.
Math.trunc (не поддерживается в Internet Explorer) — удаление дробной части без округления.

Метод JavaScript toFixed(m) для округления чисел до заданной точности:

num.toFixed(m) — округляет значение до ближайшего числа (m — число знаков после запятой), как в большую, так и в меньшую сторону, аналогично методу Math.round. Результат возвращает в виде строки.

JavaScript

value = 0.6 + 0.7; // результат 1.2999999999999998
value = value.toFixed(2); // результат 1.30 — строка (string)

value1 = 0.6 + 0.7; // результат 1.2999999999999998
value1 = +value1.toFixed(2); // результат 1.3 — число (number), приведение с помощью унарного «+»
value1 = parseFloat(value1.toFixed(2)); // результат 1.3 — число (number), приведение с помощью функции parseFloat

1
2
3
4
5
6

value=0.6+0.7;// результат 1.2999999999999998

value=value.toFixed(2);// результат 1.30 — строка (string)

value1=0.6+0.7;// результат 1.2999999999999998

value1=+value1.toFixed(2);// результат 1.3 — число (number), приведение с помощью унарного «+»

value1=parseFloat(value1.toFixed(2));// результат 1.3 — число (number), приведение с помощью функции parseFloat

Если десятичная часть короче, чем необходимо, в конец строки будут добавлены нули:

JavaScript

let num = 12.34;
alert( num.toFixed(5) ); // «12.34000», добавлены нули, чтобы получить 5 знаков после запятой

1 2	let num=12.34; alert(num.toFixed(5));// «12.34000», добавлены нули, чтобы получить 5 знаков после запятой

Альтернативный метод округления

Например, чтобы округлить число до второго знака после запятой, мы можем умножить число на 100, вызвать функцию округления и разделить обратно.

JavaScript

let num = 1.23456;

alert( Math.floor(num * 100) / 100 ); // 1.23456 -> 123.456 -> floor -> 123 -> 1.23

1
2
3

let num=1.23456;

alert(Math.floor(num*100)100);// 1.23456 -> 123.456 -> floor -> 123 -> 1.23

Basic math in javascript

Сравнение чисел

Основные математические операции

Интересный факт о strictfp

Rounding the Number

Rounding to the Nearest Integer

Rounding to Arbitrary Levels of Precision

Неточные вычисления

Сравнение чисел

Основные математические операции

Set functions #

Устройство чисел с плавающей точкой

Why Round Numbers?

Displaying on the Pixel

Improving Performance

Dealing with JavaScript’s Quirky Number Handling

Великий и могучий Math

Math.floor ()

Math.ceil ()

Math.round ()

Сравнение дробных чисел

JavaScript

Комментарии

Floor(Double)

Возвращаемое значение

Примеры

Комментарии

Как явно преобразовать строку в число?

Функция isFinite

Целая и дробная часть числа

Делится ли число нацело

Как явно преобразовать строку в число

Округление чисел в JavaScript (floor, ceil, round, trunc, toFixed)

Встроенные функции JavaScript для округления чисел до целого:

Метод JavaScript toFixed(m) для округления чисел до заданной точности: