Округление чисел

Формат чисел через контекстное меню

Нужную степень отображаемого на экране округления можно изменить и другим способом – через контекстное меню ячейки.

1. Выделяем нужную ячейку (или область, состоящую из нескольких ячеек) и кликаем по ней правой кнопкой мыши. В контекстном меню выбираем пункт “Формат ячеек…”.
2. Откроется окно, в котором в верхнем меню переходим во вкладку “Число” (по умолчанию должна быть установлена именно эта вкладка). В списке слева выбираем “Числовой” формат. Справа находим надпись “Число десятичных знаков”, рядом с которым есть текстовое поле для выбора количества знаков дробной части. Можно ввести его самостоятельно или дойти до нужного значения путем нажатия на стрелки вверх или вниз.
3. Далее нажимаем на “ОК”, после чего изменения вступят в силу.

Примечание: Также можно поставить галочку напротив надписи “Разделитель групп разрядов”, чтобы при отображении больших чисел разграничить группы разрядов.

Варианты округления 0,5 к ближайшему целому

Отдельного описания требуют правила округления для специального случая, когда (N+1)-й знак = 5, а последующие знаки равны нулю. Если во всех остальных случаях округление до ближайшего целого обеспечивает меньшую погрешность округления, то данный частный случай характерен тем, что для однократного округления формально безразлично, производить его «вверх» или «вниз» — в обоих случаях вносится погрешность ровно в 1/2 младшего разряда. Существуют следующие варианты правила округления до ближайшего целого для данного случая:

• Математическое округление — округление всегда в бо́льшую по модулю сторону (предыдущий разряд всегда увеличивается на единицу).
• Банковское округление (англ. banker’s rounding) — округление для этого случая происходит к ближайшему чётному, то есть 2,5 → 2; 3,5 → 4.
• Случайное округление — округление происходит в меньшую или большую сторону в случайном порядке, но с равной вероятностью (может использоваться в статистике). Также часто используется округление с неравными вероятностями (вероятность округления вверх равна дробной части), этот способ делает накопление ошибок случайной величиной с нулевым математическим ожиданием.
• Чередующееся округление — округление происходит в меньшую или большую сторону поочерёдно.

Во всех вариантах в случае, когда (N+1)-й знак не равен 5 или последующие знаки не равны нулю, округление происходит по обычным правилам: 2,49 → 2; 2,51 → 3.

Математическое округление просто формально соответствует общему правилу округления (см. выше). Его недостатком является то, что при округлении большого числа значений, которые далее будут обрабатываться совместно, может происходить накопление ошибки округления. Типичный пример: округление до целых рублей денежных сумм, выражаемых в рублях и копейках. В реестре из 10 000 строк (если считать копеечную часть каждой суммы случайным числом с равномерным распределением, что обычно вполне допустимо) окажется в среднем около 100 строк с суммами, содержащими в части копеек значение 50. При округлении всех таких строк по правилам математического округления «вверх» сумма «итого» по округлённому реестру окажется на 50 рублей больше точной.

Три остальных варианта как раз и придуманы для того, чтобы уменьшить общую погрешность суммы при округлении большого количества значений. Округление «до ближайшего чётного» исходит из предположения, что при большом числе округляемых значений, имеющих 0,5 в округляемом остатке, в среднем половина из них окажется слева, а половина — справа от ближайшего чётного, таким образом, ошибки округления взаимно погасятся. Строго говоря, предположение это верно лишь тогда, когда набор округляемых чисел обладает свойствами случайного ряда, что обычно верно в бухгалтерских приложениях, где речь идёт о ценах, суммах на счетах и так далее. Если же предположение будет нарушено, то и округление «до чётного» может приводить к систематическим ошибкам. Для таких случаев лучше работают два следующих метода.

Два последних варианта округления гарантируют, что примерно половина специальных значений будет округлена в одну сторону, половина — в другую. Но реализация таких методов на практике требует дополнительных усилий по организации вычислительного процесса.

• Округление в случайную сторону требует для каждой округляемой строки генерировать случайное число. При использовании псевдослучайных чисел, создаваемых линейным реккурентным методом, для генерации каждого числа требуется операция умножения, сложения и деления по модулю, что для больших объёмов данных может существенно замедлить расчёты.
• Чередующееся округление требует хранить флаг, показывающий, в какую сторону последний раз округлялось специальное значение, и при каждой операции переключать значение этого флага.

Как задать числам требуемую точность при расчетах

Предыдущие примеры затрагивали то, как настроить визуальное отображение числового значения. Но Эксель позволяет задать и точность самих операций с числами. Это полезно, например, при финансовых расчетах, где обычно используются числа только с двумя цифрами после запятой.

Для изменения данного параметра откройте вкладку “Файл” в верхнем меню программы. В новом окне найдите строку “Параметры” в списке слева и нажмите на нее.

На экране должно появиться окно настройки параметров. Здесь переходим в раздел “Дополнительно”, далее находим внизу правой части окна подраздел “При пересчете этой книги”, в котором предлагается выбрать четыре параметра. Напротив второго из них (“Задать указанную точность”) устанавливаем галочку и нажимаем “OK”.

С этого момента при расчетах будет использоваться то значение, которое вы на мониторе.

Важно: Обратите внимание, что настройка будет применена к файлу целиком, а не к отдельному листу, из которого были открыты настройки

Округление десятичных дробей

При округлении десятичных дробей следует быть особенно внимательным, поскольку десятичная дробь состоит из целой и дробной части. И каждая из этих двух частей имеет свои разряды:

Разряды целой части:

• разряд единиц;
• разряд десятков;
• разряд сотен;
• разряд тысяч.

Разряды дробной части:

• разряд десятых;
• разряд сотых;
• разряд тысячных

Рассмотрим десятичную дробь 123,456 — сто двадцать три целых четыреста пятьдесят шесть тысячных. Здесь целая часть это 123, а дробная часть 456. При этом у каждой из этих частей есть свои разряды

Очень важно не путать их:

Для целой части применяются те же правила округления, что и для обычных чисел. Отличие в том, что после округления целой части и замены нулями всех цифр после сохраняемой цифры, дробная часть полностью отбрасывается.

Например, округлим дробь 123,456 до разряда десятков. Именно до разряда десятков, а не разряда десятых

Очень важно не перепутать эти разряды. Разряд десятков располагается в целой части, а разряд десятых в дробной

Итак, мы должны округлить 123,456 до разряда десятков. Сохраняемая цифра здесь это 2, а первая из отбрасываемых цифр это 3

Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 0, 1, 2, 3 или 4, то сохраняемая цифра остаётся без изменений.

Значит сохраняемая цифра останется без изменений, а всё остальное заменится нулём. А что делать с дробной частью? Её просто отбрасывают (убирают):

123,456 ≈ 120

Теперь попробуем округлить ту же самую дробь 123,456 до разряда единиц. Сохраняемая цифра здесь будет 3, а первая из отбрасываемых цифр это 4, которая находится в дробной части:

Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 0, 1, 2, 3 или 4, то сохраняемая цифра остаётся без изменений.

Значит сохраняемая цифра останется без изменений, а всё остальное заменится нулём. Оставшаяся дробная часть будет отброшена:

123,456 ≈ 123,0

Ноль, который остался после запятой тоже можно отбросить. Значит окончательный ответ будет выглядеть следующим образом:

123,456 ≈ 123,0 ≈ 123

Теперь займёмся округлением дробных частей. Для округления дробных частей справедливы те же правила, что и для округления целых частей. Попробуем округлить дробь 123,456 до разряда десятых. В разряде десятых располагается цифра 4, значит она является сохраняемой цифрой, а первая отбрасываемая цифра это 5, которая находится в разряде сотых:

Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.

Значит сохраняемая цифра 4 увеличится на единицу, а остальная часть заменится нулями

123,456 ≈ 123,500

Попробуем округлить ту же самую дробь 123,456 до разряда сотых. Сохраняемая цифра здесь это 5, а первая из отбрасываемых цифр это 6, которая находится в разряде тысячных:

Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.

Значит сохраняемая цифра 5 увеличится на единицу, а остальная часть заменится нулями

123,456 ≈ 123,460

Понравился урок? Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Различие округления в Python 2 и Python 3

В Python 2 и Python 3 реализованы разные принципы округления.

В Python 2 используется арифметическое округление. В нем наблюдается большое количество погрешностей, что приводит к неточностям в процессе вычислений.

Во втором Python есть только 4 цифры, которые ведут к преобразованию к меньшему значению – 1, 2, 3 и 4. Также 5 цифр, которые приводят к большему значению – 5, 6, 7, 8, 9. Такое неравное распределение ведет к тому, что погрешность постоянно нарастает.

Python 2 по правилам арифметического округления преобразует число 5,685 в 5,68 до второго знака. Такая погрешность связана с тем, что десятичные цифры float в двоичном коде невозможно корректно представить.

В Python 3 используются принципы банковского округления. Это означает, что преобразование производится к ближайшему четному. В таком случае также не удается полностью избежать возникающих ошибок, но программисты добиваются точности в подсчетах.

2,5 по правилам банковского преобразования будет равно 2, а 3,5 = 4 (значения возводятся к близкому четному). Минимизировать погрешности можно благодаря практически равной вероятности, что перед пятеркой будет четное или нечетное число.

Что такое округление?

Нередко случаются ситуации, когда итогом вычисления служит бесконечное число. Это дробь с неограниченным числом знаков после запятой. Такое чаще всего возникает в результате деления чисел. Среди бесконечных дробей выделяют:

• Циклические бесконечные дроби. Это дроби, знаки после запятой у которых повторяются после определенного периода. Например, число 1,24352435 – циклическая бесконечная дробь с циклом в 4 знака.
• Бесконечная дробь, в которой знаки после запятой не повторяются.

Циклическая бесконечная дробь в математике считается определенным числом, так как каждое следующее число можно предсказать. При этом простые бесконечные дроби вычисленными не считается. Наиболее известным не вычисленным числом считается число пи, у которого на сегодняшний день вычислено 2,7 триллиона знаков после запятой.

Способы округления чисел

Для округления чисел придумано много способов, они не лишены недостатков, однако часто используются для решения задач. Разберёмся в тонкостях каждого из них.

Если используется стандартная библиотека math, то в начале кода её необходимо подключить. Сделать это можно, например, с помощью инструкции: .

math.ceil() — округление чисел в большую сторону

Функция получила своё имя от термина «ceiling», который используется в математике для описания числа, которое больше или равно заданному.

Любая дробь находится в целочисленном интервале, например, 1.2 лежит между 1 и 2. Функция определяет, какая из границ интервала наибольшая и записывает её в результат округления.

Пример:

math.ceil(5.15) # = 6
math.ceil(6.666) # = 7
math.ceil(5) # = 5

Важно помнить, что функция определяет наибольшее число с учётом знака. То есть результатом округления числа -0.9 будет 0, а не -1.

math.floor() — округление чисел в меньшую сторону

Функция округляет дробное число до ближайшего целого, которое меньше или равно исходному. Работает аналогично функции , но с округлением в противоположную сторону.

Пример:

math.floor(7.9) # = 7
math.floor(9.999) # = 9
math.floor(-6.1) # = -7

math.trunc() — отбрасывание дробной части

Возвращает целое число, не учитывая его дробную часть. То есть никакого округления не происходит, Python просто забывает о дробной части, приводя число к целочисленному виду.

Примеры:

math.trunc(5.51) # = 5
math.trunc(-6.99) # = -6

Избавиться от дробной части можно с помощью обычного преобразования числа к типу int. Такой способ полностью эквивалентен использованию .

Примеры:

int(5.51) # = 5
int(-6.99) # = -6

Нормальное округление

Python позволяет реализовать нормальное арифметическое округление, использовав функцию преобразования к типу int.

И хотя работает по другому алгоритму, результат её использования для положительных чисел полностью аналогичен выводу функции floor(), которая округляет числа «вниз». Для отрицательных аналогичен функции ceil().

Примеры:

math.floor(9.999) # = 9
int(9.999) # = 9
math.ceil(-9.999) # = -9
int(-9.999) # = -9

Чтобы с помощью функции int() округлить число по математическим правилам, необходимо добавить к нему 0.5, если оно положительное, и -0.5, если оно отрицательное.

Тогда операция принимает такой вид: int(num + (0.5 if num > 0 else -0.5)). Чтобы каждый раз не писать условие, удобно сделать отдельную функцию:

def int_r(num):
    num = int(num + (0.5 if num > 0 else -0.5))
    return num

Функция работает также, как стандартная функция округление во второй версии Python (арифметическое округление).

Примеры:

int_r(11.5) # = 12
int_r(11.4) # = 11
int_r(-0.991) # = -1
int_r(1.391) # = 1

round() — округление чисел

round() — стандартная функция округления в языке Python. Она не всегда работает так, как ожидается, а её алгоритм различается в разных версиях Python.

В Python 2

Во второй версии Python используется арифметическое округление. Оно обладает постоянно растущей погрешностью, что приводит к появлению неточностей и ошибок.

Увеличение погрешности вызвано неравным количеством цифр, определяющих, в какую сторону округлять. Всего 4 цифры на конце приводят к округлению «вниз», и 5 цифр к округлению «вверх».

Помимо этого, могут быть неточности, например, если округлить число 2.675 до второго знака, получится число 2.67 вместо 2.68. Это происходит из-за невозможности точно представить десятичные числа типа «float» в двоичном коде.

В Python 3

В третьей версии Python используется банковское округление. Это значит, что округление происходит до самого близкого чётного.

Такой подход не избавляет от ошибок полностью, но уменьшает шанс их возникновения и позволяет программисту добиться большей точности при вычислениях.

Примеры:

round(3.5) # = 4
round(9.5) # = 10
round(6.5) # = 6
round(-6.5) # = -6
round(-7.5) # = -8

Но если вам по каким то причинам нужно округление как в Python 2, то можно воспользоваться функцией написанной нами выше на основе приведения к целому числу.

Округление до сотых

У функции есть ещё один аргумент. Он показывает до какого количества знаков после запятой следует округлять. Таким образом, если нам надо в Python округлить до сотых, этому параметру следует задать значение 2.

Пример округления до нужного знака:

round(3.555, 2) # = 3.56
round(9.515,1) # = 9.5
round(6.657,2) # = 6.66

Округление десятичных дробей

Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которой можно представить число. Есть два формата записи:

• обыкновенный вид — 1/2 или a/b,
• десятичный вид — 0,5.

В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. Выходит, что десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Такую дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:

• 0,7
• 6,35
• 9,891

При округлении десятичных дробей следует быть особенно внимательным, потому что десятичная дробь состоит из целой и дробной части. И у каждой из этих частей есть свои разряды:

Разряды целой части:

• разряд единиц;
• разряд десятков;
• разряд сотен;
• разряд тысяч.

Разряды дробной части:

• разряд десятых;
• разряд сотых;
• разряд тысячных.

Разряд — это позиция, место расположения цифры в записи натурального числа. У каждого разряда есть свое название. Слева всегда располагаются старшие разряды, а справа — младшие.

Рассмотрим десятичную дробь 7396,1248. Здесь целая часть — 7396, а дробная — 1248

При этом у каждой из них есть свои разряды, которые важно не перепутать:

Чтобы округлить десятичную дробь, нужно в записи числа выбрать разряд, до которого производится округление.

То натуральное число, к которому дробь ближе, называют округленным значением числа.

Цифра, которая записана в данном разряде:

• не меняется, если следующая за ней справа цифра — 0,1, 2, 3 или 4;
• увеличивается на единицу, если за ней справа следует цифра — 5, 6, 7, 8 или 9.

Как округлить до целых. Заменить десятичную дробь ближайшим к ней целым числом. Ближайшим будет наименьшее расстояние. При этом если расстояние до приближенного значения числа с недостатком и расстояние до приближенного значения числа с избытком равны, то округляют в большую сторону.

Как округлить до десятых. Оставить одну цифру после запятой. Изи!

Как округлить до сотых. Оставить две цифры после запятой.

Все цифры, которые стоят справа от данного разряда, заменяются нулями. Если эти нули стоят в дробной части числа, то их можно не писать.

Комментарии

Поведение этого метода соответствует стандарту IEEE 754, разделу 4.The behavior of this method follows IEEE Standard 754, section 4. Этот тип округления иногда называют округлением в сторону отрицательной бесконечности.This kind of rounding is sometimes called rounding toward negative infinity.

Floor(Double)

Возвращает наибольшее целое число, которое меньше или равно заданному числу с плавающей запятой двойной точности.Returns the largest integral value less than or equal to the specified double-precision floating-point number.

d

Double

Число двойной точности с плавающей запятой.A double-precision floating-point number.

Возвращаемое значение

Double

Наибольшее целое число, которое меньше или равно .The largest integral value less than or equal to . Если значение параметра равно NaN, NegativeInfinity или PositiveInfinity, возвращается это значение.If is equal to NaN, NegativeInfinity, or PositiveInfinity, that value is returned.

Примеры

В следующем примере показан метод и его отличие от метода.The following example illustrates the method and contrasts it with the method.

Комментарии

Поведение этого метода соответствует стандарту IEEE 754, разделу 4.The behavior of this method follows IEEE Standard 754, section 4. Этот тип округления иногда называют округлением в сторону отрицательной бесконечности.This kind of rounding is sometimes called rounding toward negative infinity. Иными словами, если является положительным, любой дробный компонент усекается.In other words, if is positive, any fractional component is truncated. Если имеет отрицательное значение, присутствие любого компонента дробной части приводит к округлению его до меньшего целого числа.If is negative, the presence of any fractional component causes it to be rounded to the smaller integer. Операция этого метода отличается от Ceiling метода, который поддерживает округление в сторону положительной бесконечности.The operation of this method differs from the Ceiling method, which supports rounding toward positive infinity.

Начиная с Visual Basic 15,8, производительность преобразования типа «двойное в целое число» оптимизирована, если передать значение, возвращаемое методом, в любую функцию целочисленного преобразованияили если значение Double, возвращаемое, автоматически преобразуется в целое число с параметром Option-on , равным OFF.Starting with Visual Basic 15.8, the performance of Double-to-integer conversion is optimized if you pass the value returned by the method to the any of the integral conversion functions, or if the Double value returned by is automatically converted to an integer with Option Strict set to Off. Эта оптимизация позволяет коду выполняться быстрее — до двух раз быстрее для кода, который выполняет большое количество преобразований в целочисленные типы.This optimization allows code to run faster — up to twice as fast for code that does a large number of conversions to integer types. В следующем примере показаны оптимизированные преобразования:The following example illustrates such optimized conversions:

Стандартная функция

Дробные числа в электронных таблицах Excel можно выводить на экран с разной степенью точности:

• самый простой способ – на вкладке «Главная» нажимаем кнопки «Увеличить разрядность» или «Уменьшить разрядность»;
• щелкаем правой кнопкой мыши по ячейке, в раскрывшемся меню выбираем «Формат ячеек…», далее вкладка «Число», выбираем формат «Числовой», определяем, сколько будет десятичных знаков после запятой (по умолчанию предлагается 2 знака);
• щелкаем ячейку, на вкладке «Главная» выбираем «Числовой», либо идем на «Другие числовые форматы…» и там настраиваем.

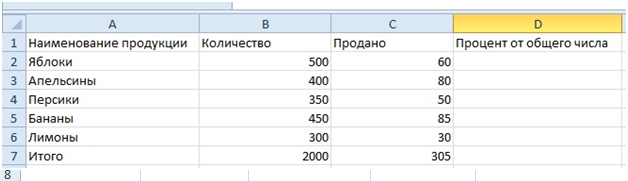
Вот как выглядит дробь 0,129, если менять количество десятичных знаков после запятой в формате ячейки: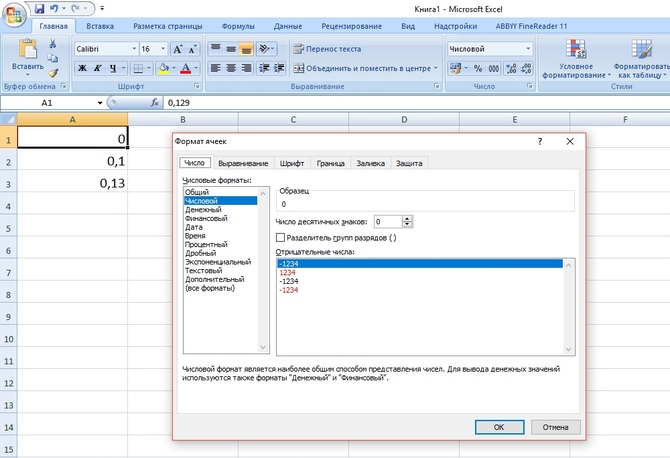

Обратите внимание, в A1,A2,A3 записано одно и то же значение, меняется только форма представления. При дальнейших расчетах будет использоваться не величина, видимая на экране, а исходная

Начинающего пользователя электронных таблиц это может слегка запутать. Чтобы реально изменить значение, необходимо использовать специальные функции, их в Excel несколько.

Правило встречается в следующих упражнениях:

5 класс

Задание 1274,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1275,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1324,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1368,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1411,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1524,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Номер 856,
Мерзляк, Полонский, Якир, Учебник

Номер 857,
Мерзляк, Полонский, Якир, Учебник

Номер 5,
Мерзляк, Полонский, Якир, Учебник

Номер 922,
Мерзляк, Полонский, Якир, Учебник

6 класс

Номер 1,
Мерзляк, Полонский, Якир, Учебник

Задание 236,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 628,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 629,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 645,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 876,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1198,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1223,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1504,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1580,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Округление чисел

Для нахождения приближенного значения применяется такое действие как округление чисел.

Слово «округление» говорит само за себя. Округлить число значит сделать его круглым. Круглым называется число, которое оканчивается нулём. Например, следующие числа являются круглыми:

10, 20, 30, 100, 300, 700, 1000

Любое число можно сделать круглым. Процедуру, при которой число делают круглым, называют округлением числá.

Мы уже занимались «округлением» чисел, когда делили большие числа. Напомним, что для этого мы оставляли без изменения цифру, образующую старший разряд, а остальные цифры заменяли нулями. Но это были лишь наброски, которые мы делали для облегчения деления. Своего рода лайфхак. По факту, это даже не являлось округлением чисел. Именно поэтому в начале данного абзаца мы взяли слово округление в кавычки.

На самом деле, суть округления заключается в том, чтобы найти ближайшее значение от исходного. При этом, число может быть округлено до определённого разряда — до разряда десятков, разряда сотен, разряда тысяч.

Рассмотрим простой пример на округление. Дано число 17. Требуется округлить его до разряда десятков.

Не забегая вперёд попробуем понять, что означает «округлить до разряда десятков». Когда говорят округлить число 17, то надо понимать, что от нас требуют найти ближайшее круглое число от числá 17. Причём в ходе этого поиска возможно изменения коснутся и той цифры, которая располагается в разряде десятков числá 17 (т.е цифры 1).

Предстáвим числа от 10 до 20 с помощью следующего рисунка:

На рисунке видно, что для числá 17 ближайшее круглое число это число 20. Значит ответ к задаче таким и будет: «17 приближённо равно 20″

17 ≈ 20

Мы нашли приближённое значение для 17, то есть округлили его до разряда десятков. Видно, что после округления в разряде десятков появилась новая цифра 2.

Попробуем найти приближённое число для числа 12. Для этого снова предстáвим числа от 10 до 20 с помощью рисунка:

На рисунке видно, что ближайшее круглое число для 12 это число 10. Значит ответ к задаче таким и будет: 12 приближённо равно 10

12 ≈ 10

Мы нашли приближённое значение для 12, то есть округлили его до разряда десятков. В этот раз цифра 1, которая стояла в разряде десятков в числе 12, не пострадала от округления. Почему так получилось мы расскажем позже.

Попробуем найти ближайшее число для числá 15. Снова предстáвим числа от 10 до 20 с помощью рисунка:

На рисунке видно, что число 15 одинаково удалено от круглых чисел 10 и 20. Возникает вопрос: которое из этих круглых чисел будет приближённым значением для числа 15? Для таких случаев условились принимать бóльшее число за приближённое. 20 больше чем 10, поэтому приближённое значение для 15 будет число 20

15 ≈ 20

Округлять можно и большие числа. Естественно, для них делать рисунки и изображать числа не представляется возможным. Для них существует свой способ. Например, округлим число 1456 до разряда десятков.

Итак, мы должны округлить 1456 до разряда десятков. Разряд десятков начинается на пятёрке:

Теперь о существовании первых цифр 1 и 4 временно забываем. Остается число 56

Теперь смотрим, какое круглое число находится ближе к числу 56. Очевидно, что ближайшее круглое число для 56 это число 60. Значит заменяем число 56 на число 60

Значит при округлении числа 1456 до разряда десятков полýчим 1460

1456 ≈ 1460

Видно, что после округления числа 1456 до разряда десятков, изменения коснулись и самогó разряда десятков. В новом полученном числе в разряде десятков теперь располагается цифра 6, а не 5.

Округлять числа можно не только до разряда десятков. Округлять число можно до разряда сотен, тысяч, десятков тысяч и так далее.

После того, как станóвится ясно, что округление это ни что иное как поиск ближáйшего числá, можно применять готовые правила, которые значительно облегчают округление чисел.