Построение графиков в mathcad

Добавление шестого измерения

Форма маркера отлично подходит для визуализации категорий. Plotly даёт на выбор 10 различных фигур для 3D графика (звёздочка, круг, квадрат и т.д.). Таким образом, в качестве формы можно показать до 10 различных значений.

У нас есть характеристика num-of-doors, которая содержит целые числа — количество дверей (2 или 4). Преобразуем эти значения в фигуры: квадрат для 4 дверей, круг для 2 дверей. Используется параметр markersymbol функции Scatter3D.

Наблюдения: такое чувство, что у всех самых дешёвых машин по 4 двери (круги). Продолжая изучать график, можно будет сделать больше предположений и выводов.

6D график с формой маркера в качестве шестого измерения (количество дверей)

Построение эпюры в mathcad

Чтобы построить классическую эпюру в mathcad нужно выполнить следующие действия:- ввести функцию в виде y = f(x), как это показано в примерах выше;
— ввести такназываемую ранжинрованную переменную в виде i = a, a-dt..b с определенным шагом dt;
— создать поле графика и ввести туда функции f(x) и f(i) с соответствующими аргументами
— настроить визуализацию функции f(i) в соответствии с требованиями к оформлению эпюр в вашем ВУЗе или компании

Ранжированная переменная по сути является матрицей-столбцом, разница лишь в том, что значение элементов в нее входящих представляют из себя определенную закономерность или последовательность чисел. Ранжированную переменную можно ввести воспользовавшись кнопкой Range Variable из панели Matrix. Первый маркер отвечает за начальное значение последовательности, второй — за конечное. По умолчаию шаг последовательности равен 1. Если после первого элемента ввести символ запятой и в появившемся маркере ввести следующее число вашей последовательности, то таким образом вы определите шаг, с которым будет заполняться ваша последовательность

Обратите внимание на пример ниже.

Рис. 8. Ввод ранжированной переменной

Ранжированные переменные можно использовать для построения эпюр распределения физических величин. Для этого постройте ваш исходный график одним из методов, описанных выше. Пусть это будет график f(x):=x^2. Затем создайте ранжированную переменную с шагом 0.5 как указано в примере ниже

Рис. 9. Ввод ранжированной переменной

Далее создайте поле для графика и около оси ординат введите две функции: f(x) и f(i). Под осью абсцисс также введите соответсвующие аргументы: x и i. Вы должны увидет обычную параболу как на рисунке ниже

Рис. 10. Построение эпюры. Шаг 1

Для получения эпюры нужно настроить отображение функции f(i) в свойствах графика. Щелкните 2 раза по графику чтобы вызвать меню настройки отображения графика. Перейдите во вкладку traces. В списке Legend Label найдите имя trace 2. В столбце Type для trace 2 из выпадающего списка выберете тип графика stem. В столбце Symbol уберите отображение элементов. Во вкладке X-Y Axes выберете для Axis Style тип Crossed. Нажмите ОК и вы увидете эпюру. Вы можете настроить ее внешний вид по желанию.

Рис. 11. Построение эпюры. Шаг 2

В итоге вы увидите, что на графике появились вертикальные линии, которые распределены по оси абсцисс с шагом, который вы указали в ранжированной переменной. Изменяя параметры этой переменной можно настроить отображение эпюры. Эпюра готова (см. рис. 12)

Рис. 12. Построение эпюры. Шаг 3

Как построить объемную диаграмму в Excel

Чтобы вставить любую объемную диаграмму, необходимо выделить ряды с исходными данными, перейти на вкладку «Вставка» и выбрать тип в группе «Диаграммы».

Таблица с исходными данными:

Построим на ее основе объемную гистограмму. Выбор для этого типа диаграммы достаточно разнообразен:

В объемных гистограммах появляется третья ось (кроме вертикальной и горизонтальной) – ось глубины. Их все пользователь может изменить. В диаграммах подобного типа сопоставляются значения по горизонтальной оси и оси глубины.

Добавим в таблицу еще один ряд данных.

Построим объемную цилиндрическую гистограмму с тремя осями. С ее помощью сравним точки данных по категориям и по рядам.

В программе Excel есть только один тип объемного графика.

Каждый ряд данных в таком графике представляет собой объемную ленту. Здесь тоже появляется третья ось – ось глубины.

Объемная круговая диаграмма в Excel иллюстрирует вклад каждого значения в общий итог в объемном формате.

Огромное преимущество таких диаграмм – возможность отделить, «вытащить» какую-либо область, чтобы заострить на ней внимание. В объемную круговую диаграмму можно включить только один ряд данных

Посмотрим, как отделяется сектор

В объемную круговую диаграмму можно включить только один ряд данных. Посмотрим, как отделяется сектор.

Добавим подписи данных на области круга (выделить диаграмму – перейти на вкладку «Макет» — «Подписи данных»).

Заострим внимание на товаре, который в анализируемом периоде продавался хуже всего. Щелкнем мышкой по сектору с надписью «19»

И, удерживая мышкой данную область, протянем ее в сторону.

Чтобы сектора были хорошо видны, немного развернем их, изменим перспективу объемной фигуры. Снова заходим на вкладку «Макет». Выбираем «Поворот объемной фигуры» в группе «Фон». Передвигаем открывшееся окно так, чтобы была видна диаграмма. Устанавливаем градусы поворота, отображения горизонтальной и вертикальной оси.

В примере так:

Фигура больше развернулась к нам «лицом»:

Для выделения каждого значения в общей сумме данных применяется объемная разрезанная круговая диаграмма.

В данном случае перемещать вручную области невозможно. Но изменять настройки разреза для отдельного либо для каждого сектора можно.

Сгруппированные линейчатые объемные диаграммы в Excel дают возможность пользователю сопоставить величины по категориям. На подобных графиках категории отображаются по вертикали, а значения – по горизонтали.

В таких диаграммах применяются объемные прямоугольники с горизонтальным направлением. Но выполнить трехмерную проекцию с использованием данного типа нельзя (ось глубины отсутствует).

Чтобы показать вклад каждой величины из ряда данных в общую сумму значений, применяют объемную линейчатую диаграмму с накоплением.

Другие горизонтальные виды объемных форматов – цилиндрические, конические, пирамидальные. Доступны те же варианты: с группировкой, с накоплением, нормированные с накоплением (для вывода доли в процентах).

Объемная диаграмма с областями показывает изменение значения с течением времени либо по подгруппам. В нашем примере – по видам товаров.

В диаграмме с областями тоже имеется ось глубины, которая меняется при необходимости.

Самым привлекательным трехмерным изображением является поверхностная диаграмма. Для наших рядов данных она будет выглядеть так:

Поверхностная диаграмма позволяет сопоставить два набора данных и найти оптимальные комбинации. Одна величина имеет два измерения. Ее изменение показано в виде поверхности. Цветные полосы разделяют значения, а не отображают ряда данных.

Такие диаграммы хорошо использовать для визуализации зависимости между большими объемами значений. Когда другие типы просто не подходят.

Нахождение возрастания и убывания, точек экстремума

Для решениянеравенства применяются промежутки возрастания и убывания с условиями f'(x)≥ и f'(x)≤ соответственно.

Определение 1

Стационарные точки – это такие точки, которые обращают производную в ноль.

Критические точки  — это внутренние точки из области определения, где производная функции равняется нулю или не существует.

При решении необходимо учитывать следующие замечания:

• при  имеющихся промежутках возрастания  и убывания неравенства вида  f'(x)> критические точки в решение не включаются;
• точки, в которых функция определена без конечной производной , необходимо включать в промежутки возрастания и убывания (к примеру, y=x3, где точка х= делает функцию определенной, производная имеет значение бесконечности в этой точке, y’=13·x23, y'()=1=∞, х= включается в промежуток возрастания);
• во избежание разногласий рекомендовано пользоваться математической литературой, которая рекомендована министерством образования.

Включение критических точек в промежутки возрастания и убывания в том случае, если они удовлетворяют области определения функции.

Определение 2

Для определения промежутков возрастания и убывания функции необходимо найти:

• производную;
• критические точки;
• разбить область определения при помощи критических точек на интервалы;
• определить знак производной на каждом из промежутков, где + является возрастанием, а — является убыванием.

Пример 3

Найти производную на области определения  f'(x)=x2′(4×2-1)-x24x2-1′(4×2-1)2=-2x(4×2-1)2.

Решение

Для решения нужно:

• найти стационарные точки, данный пример располагает х=;
• найти нули знаменателя, пример принимает значение ноль при x=±12.

Выставляем точки на числовой оси для определения производной   на каждом промежутке. Для этого достаточно взять любую точку из промежутка и произвести вычисление. При положительном результате на графике изображаем +, что означает возрастание функции, а — означает ее убывание.

Например, f'(-1)=-2·(-1)4-12-12=29>, значит, первый интервал слева имеет знак +. Рассмотрим на числовой прямой.

Ответ:

• происходит возрастание функции на промежутке -∞; -12 и (-12; ;
• происходит убывание на промежутке ; 12) и 12; +∞. 

На схеме при помощи + и — изображается положительность и отрицательность функции, а стрелочки – убывание и возрастание.

Точки  экстремума функции – точки, где функция определена и через которые производная меняет знак.

Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!

Описать задание

Пример 4

Если рассмотреть пример, где х=, тогда значение функции в ней равняется f()=24·2-1=.  При перемене знака производной с + на — и прохождении через точку х=, тогда точка с координатами (; ) считается точкой максимума. При перемене знака с — на + получаем точку минимума.

Два в одном — как сделать?

Хитрости » 1 Май 2011       Дмитрий       227396 просмотров

Если Вы еще не умеете строить диаграммы и не знаете где это советую почитать статью Общие сведения о диаграммах и графиках

Для построения такой диаграммы нам понадобится таблица с исходными данными, и не менее двух рядов данных. Для тренировки вы можете скачать пример файла внизу статьи — там есть все исходные данные. Для начала необходимо определить тип нашей диаграммы.

Важно: если вы планируете в своей диаграмме использовать тип Гистограмма(Columns), то при создании диаграммы необходимо выбрать именно этот тип диаграммы. А затем уже добавлять остальные типы диаграмм, т.к

попытки назначить тип Гистограмма(Columns) после всех остальных приведут к тому, что все ряды станут типа Гистограмма(Columns). Притом без каких-либо предупреждений.
Так же следует помнить, что нельзя совместить объемные и плоские типы диаграмм.

Но при любой попытке совмещения плоских и объемных типов Excel сам предупредит об этом, так что это не так страшно.

После выбора первоначального типа диаграммы щелкаем мышкой один раз по одному из рядов данных на диаграмме(выделятся все столбики данного ряда). Правая кнопка мыши:

• Excel 2003 — Тип диаграммы (Chart Type)
• Excel 2007-2010 — Изменить тип диаграммы для ряда (Change Series Chart Type)

Выбираем тип и смотрим как изменилась диаграмма.

Маленький нюанс: если ваши данные имеют в одной таблице большую разницу между собой (например суммы продаж в рублях и количество проданного товара) и вы хотите сравнить эти данные совместив в одной диаграмме — то изначально у вас ничего не выйдет, т.к.

разница в числовых данных между рядами будет отличаться в десятки, а то и сотни раз. Что сделает данные по количеству практически не заметными. Чтобы этого избежать можно воспользоваться интересной возможностью — построить эти данные по другой оси.

Правая кнопка мыши по ряду-Формат ряда данных(Format Data Series)-группа Параметры ряда(Series Option)—По вспомогательной оси(Secondary Axis):

Так же если щелкнуть по ряду данных правой кнопкой мыши и выбрать уже Формат ряда данных(Format Data Series), то можно побродить по другим параметрам и изменить цвет заливки для отдельного ряда, границы, добавить тени и т.п. Это дает довольно большой простор для творчества и рассказать ту больше особо нечего — надо пробовать и творить

Скачать пример:

  Tips_Chart_Two_In_One.xls (47,0 KiB, 13 836 скачиваний)

Статья помогла? Поделись ссылкой с друзьями!

Как построить график зависимости в Excel?

График зависимости по сути своей и есть график функции; речь может идти лишь о сложности математического выражения, в остальном порядок создания визуальных представлений остаётся тем же. Чтобы показать, как построить график сложной зависимости нескольких параметров от исходных значений, ниже будет приведён ещё один небольшой пример.

Пусть параметр Y зависит от X в виде y = x3 + 3x – 5; Z — в виде z = x/2 + x2; наконец, зависимость R — выражается в виде набора несистематизированных значений.

Тогда, чтобы построить сводный график зависимости, необходимо:

Составить в Excel таблицу с заголовками, отображающими суть каждой зависимости. Пусть для примера это будут просто X, Y, Z и R. В этой таблице сразу можно задать значения оси абсцисс (X) и параметра R, не выражаемого известной функцией.

Ввести в верхней ячейке столбца Y формулу, нажать клавишу Enter и «растянуть» значения на весь диапазон X.

То же проделать для столбца Z. Как можно убедиться, при изменении любого параметра X будут меняться соответствующие значению Y и Z, в то время как R останется неизменным.

Выделить три столбца производных от X и построить, как было рассказано раньше, график — гладкий, с маркерами или в виде точек.

Если одна из функций мешает наблюдать за изменениями остальных, её можно удалить с графика, выделив щелчком мыши и нажав клавишу Delete.

Научившись строить графики в Экселе, пользователь может перейти к следующей важной задаче — попытаться сделать оформление каждой зависимости красивым и рациональным

Понятие графика функции

Графиком функции y = f(x) называется множество точек (x; y), координаты которых связаны соотношением y = f(x). Само равенство y = f(x) называется уравнением данного графика.

График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу.

Проще говоря, график функции показывает множество всех точек, координаты которых можно найти, просто подставив в функцию любые числа вместо x.

Для примера возьмём самую простую функцию, в которой аргумент равен значению функции, то есть y = x.

В этом случае нам не придётся вычислять для каждого аргумента значение функции, так как они равны, поэтому у всех точек нашего графика абсцисса будет равна ординате.

Отметим любые три точки на координатной плоскости, например: L (-2; -2), M (0; 0) и N (1; 1).

Если мы последовательно от наименьшего значения аргумента к большему соединим отмеченные точки, то у нас получится прямая линия. Значит графиком функции y = x является прямая. На графике это выглядит так:

Надпись на чертеже y = x — это уравнение графика. Ставить надпись с уравнением на чертеже удобно, чтобы не запутаться в решении задач.

Важно отметить, что прямая линия бесконечна в обе стороны. Хоть мы и называем часть прямой графиком функции, на самом деле на чертеже изображена только малая часть графика

Не обязательно делать чертеж на целый тетрадный лист, можно выбрать удобный для вас масштаб, который отразит суть задания.

Масштабный сетевой график

1. Вычислить табличным методом все основные характеристики работ и событий, найти критический путь и его продолжительность.
2. Построить масштабный сетевой график.
3. Оценить вероятность выполнения всего комплекса работ за 30 дней.
4. Оценить максимально возможный срок выполнения всего комплекса работ с вероятностью 95%.

Код работы ( i,j)	Продолжительность
tmin (i,j)	tmax (i,j)
1,2	5	10
1,4	2	7
1,5	1	6
2,3	2	4,5
2,8	9	19
3,4	1	3,5
3,6	9	19
4,7	4	6,5
5,7	2	7
6,8	7	12
7,8	5	7,5

Решение находим с помощью сервиса Сетевая модель. В нашем задании продолжительность выполнения работы задаётся двумя оценками – минимальная и максимальная. Минимальная оценка характеризует продолжительность выполнения работы при наиболее благоприятных обстоятельствах, а максимальная t_max(i,j) – при наиболее неблагоприятных условиях. Продолжительность работы в этом случае рассматривается, как случайная величина, которая в результате реализации может принять любое значение в заданном интервале. Такие оценки называются вероятностными (случайными), и их ожидаемое значение t_ож(i,j) оценивается по формуле
t_ож(i,j)=(3 t_min(i,j)+2 t_max (i,j))/5
Для характеристики степени разброса возможных значений вокруг ожидаемого уровня используется показатель дисперсии:
S2(i,j)=0,04(t_max(i,j)-t_min(i,j))2Рассчитаем ожидаемое значение и показатель дисперсии.
t_ож(1,2)=(3*5+2*10)/5=7
t_ож(1,4)=(3*2+2*7)/5=4
t_ож(1,5)=(3*1+2*6)/5=3
t_ож(2,3)=(3*2+2*4,5)/5=3
t_ож(2,8)=(3*9+2*19)/5=13
t_ож(3,4)=(3*1+2*3,5)/5=2
t_ож(3,6)=(3*9+2*19)/5=13
t_ож(4,7)=(3*4+2*6,5)/5=5
t_ож(5,7)=(3*2+2*7)/5=4
t_ож(6,8)=(3*7+2*12)/5=9
t_ож(7,8)=(3*5+2*7,5)/5=6
S2(1,2)=0,04*(10-5)2=1
S2(1,4)=0,04*(7-2)2=1
S2(1,5)=0,04*(6-1)2=1
S2(2,3)=0,04*(4,5-1)2=0,25
S2(2,8)=0,04*(19-9)2=4
S2(3,4)=0,04*(3,5-1)2=6,25
S2(3,6)=0,04*(19-9)2=4
S2(4,7)=0,04*(6,5-4)2=0,25
S2(5,7)=0,04*(7-2)2=1
S2(6,8)=0,04*(12-7)2=1
S2(7,8)=0,04*(7,5-5)2=0,25

Полученные данные занесем в таблицу.

Таблица – Сетевая модель.

Работа ( i,j)	Продолжительность	Ожидаемая продолжительность tож(i,j)	Дисперсия S2(i,j)
tmin (i,j)	tmax (i,j)
1,2	5	10	7	1
1,4	2	7	4	1
1,5	1	6	3	1
2,3	2	4,5	3	0,25
2,8	9	19	13	4
3,4	1	3,5	2	6,25
3,6	9	19	13	4
4,7	4	6,5	5	0,25
5,7	2	7	4	1
6,8	7	12	9	1
7,8	5	7,5	6	0,25

КПР	Код работы (i,j)	Продолжительность работы t(i, j)	Ранние сроки	Поздние сроки	Резервы времени
tрн(i,j)	tро(i,j)	tпн(i,j)	tпо(i,j)	Rп	Rc
1	2	3	4	5	6	7	8	9
1,2	7	7	7
1,4	4	4	17	21	17	8
1,5	3	3	19	22	19
1	2,3	3	7	10	7	10
1	2,8	13	7	20	19	32	12	12
1	3,4	2	10	12	19	21	9
1	3,6	13	10	23	10	23
2	4,7	5	12	17	21	26	9
1	5,7	4	3	7	22	26	19	10
1	6,8	9	23	32	23	32
2	7,8	6	17	23	26	32	9	9

_кр

Рисунок — Масштабный график сетевой модели

P(t_кр
где Z=(Т-Т_кр)/S_крZ- нормативное отклонение случайной величины, S_кр – среднеквадратическое отклонение, вычисляемое как корень квадратный из дисперсии продолжительности критического пути.
Соответствие между Z и Ф(Z) представлено в таблице.

Таблица — Таблица стандартного нормального распределения.

Z	F(Z)	Z	F(Z)	Z	F(Z)
0.0000	1.0	0.6827	2.0	0.9643
0.1	0.0797	1.1	0.7287	2.1	0.9722
0.2	0.1585	1.2	0.7699	2.2	0.9786
0.3	0.2358	1.3	0.8064	2.3	0.9836
0.4	0.3108	1.4	0.8385	2.4	0.9876
0.5	0.3829	1.5	0.8664	2.5	0.9907
0.6	0.4515	1.6	0.8904	2.6	0.9931
0.7	0.5161	1.7	0.9104	2.7	0.9949
0.8	0.5763	1.8	0.9281	2.8	0.9963
0.9	0.6319	1.9	0.9545	2.9	0.9973

Критический путь проходит по работам (1,2)(2,3)(3,6)(3,8). 
Дисперсия критического пути:
S2­(L_кр)= S2(1,2)+ S2(2,3)+ S2(3,6)+S2(6,8)=1+0,25+4+1=6,25
S(L_кр)=2,5
p(t_кр<30)=0,5+0,5Ф((30-32)/2,5)=0,5-0,5Ф(0,8) = 0,5-0,5*0,5763=0,5-0,28815=0,213
Вероятность того, что весь комплекс работ будет выполнен не более чем за 30 дней, составляет 21,3%.
Для определения максимально возможного срока выполнения всего комплекса работ с надежностью 95% будем использовать следующую формулу:

T=Т_кр+Z*S_кр

Для решения поставленной задачи найдем значение аргумента Z, которое соответствует заданной вероятности 95% (значению графы Ф(Z)  0,9545*100% в таблице 5 соответствует Z=1,9).
T=32+1,9*2,5=36,8
Максимальный срок выполнения всего комплекса работ при заданном уровне вероятности 95% составляет всего 36,8 дня.

Построение графика функции

Чтобы понять, как строить графики функций, потренируемся на примерах.

Задача 1. Построим график функции

Как решаем:

Упростим формулу функции:

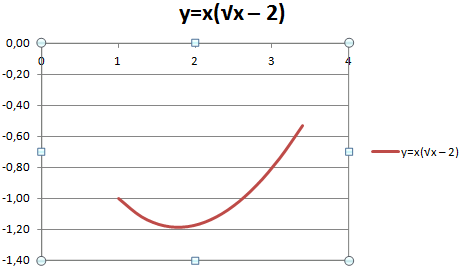
Задача 2. Построим график функции

Как решаем:

Выделим в формуле функции целую часть:

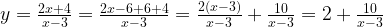
График функции — гипербола, сдвинутая на 3 вправо по x и на 2 вверх по y и растянутая в 10 раз по сравнению с графиком функции

Выделение целой части — полезный прием, который применяется в решении неравенств, построении графиков и оценке целых величин.

Задача 3. По виду графика определить знаки коэффициентов общего вида функции y = ax2 + bx + c.

Как решаем:

Вспомним, как параметры a, b и c определяют положение параболы.

1. Ветви вниз, следовательно, a < 0.

   Точка пересечения с осью Oy — c = 0.

   Координата вершины

2. Ветви вверх, следовательно, a > 0.

   Точка пересечения с осью Oy — c = 0.

   Координата вершины , т.к. неизвестное число при делении на положительное дает отрицательный результат, то это число отрицательное, следовательно, b > 0.

3. Ветви вниз, следовательно, a < 0.

   Точка пересечения с осью Oy — c > 0.

   Координата вершины , т.к. неизвестное число при делении на отрицательное дает в результате положительное, то это число отрицательное, следовательно, b < 0.

Задача 4. Построить графики функций:

а) y = 3x — 1

б) y = -x + 2

в) y = 2x

г) y = -1

Как решаем:

Воспользуемся методом построения линейных функций «по точкам».

а) y = 3x — 1

x	y
-1
1	2

Как видим, k = 3 > 0 и угол наклона к оси Ox острый, b = -1 — смещение по оси Oy.

б) y = -x + 2

x	y
2
1	1

k = -1 > 0 и b = 2 можно сделать аналогичные выводы, как и в первом пункте.

в) y = 2x

x	y
1	2

k = 2 > 0 — угол наклона к оси Ox острый, B = 0 — график проходит через начало координат.

г) y = -1

k = 0 — константная функция, прямая проходит через точку b = -1 и параллельно оси Ox.

Задача 5. Построить график функции

Как решаем:

Это дробно-рациональная функция. Область определения функции D(y): x ≠ 4; x ≠ 0.

Нули функции: 3, 2, 6.

Промежутки знакопостоянства функции определим с помощью метода интервалов.

Вертикальные асимптоты: x = 0, x = 4.

Если x стремится к бесконечности, то у стремится к 1. Значит, y = 1 — горизонтальная асимптота.

Вот так выглядит график:

Задача 6. Построить графики функций:

а) y = x² + 1

б)

в) y = (x — 1)² + 2

г)

д)

Как решаем:

Когда сложная функция получена из простейшей через несколько преобразований, то преобразования графиков можно выполнить в порядке арифметических действий с аргументом.

а)

Преобразование в одно действие типа f(x) + a.

y = x²

Сдвигаем график вверх на 1:

y = x² + 1

б)

Преобразование в одно действие типа f(x — a).

y = √x

Сдвигаем график вправо на 1:

y = √x — 1

в) y = (x — 1)² + 2

В этом примере два преобразования, выполним их в порядке действий: сначала действия в скобках f(x — a), затем сложение f(x) + a.

y = x²

Сдвигаем график вправо на 1:

y = (x — 1)²

Сдвигаем график вверх на 2:

y = (x — 1)² + 2

г)

Преобразование в одно действие типа

y = cos(x)

Растягиваем график в 2 раза от оси ординат вдоль оси абсцисс:

д)

Мы видим три преобразования вида f(ax), f (x + a), -f(x).

Чтобы выполнить преобразования, посмотрим на порядок действий: сначала умножаем, затем складываем, а уже потом меняем знак. Чтобы применить умножение ко всему аргументу модуля в целом, вынесем двойку за скобки в модуле.

Сжимаем график в два раза вдоль оси абсцисс:

Сдвигаем график влево на 1/2 вдоль оси абсцисс:

Отражаем график симметрично относительно оси абсцисс:

В детской школе Skysmart учиники чертят графики на специальной онлайн-доске. Учитель видит, как размышляет ученик и может вовремя его направить в нужную сторону.

Запишитесь на бесплатный вводный урок математики и занимайтесь в современном формате и с поддержкой заботливых учителей.

Как строить графики

Для примера возьму такие данные. Есть сотрудники, и количество товара, которое они продали, за определенный месяц. График поможет быстрее понять, какой сотрудник продал больше всего товаров за определенный месяц, или за весь период.

Поставьте курсор в нужном месте документа. Затем перейдите на вкладку «Вставка» и в разделе «Иллюстрации», нажмите на кнопочку с изображением диаграммы.

Появится вот такое окно, как на скриншоте ниже. В нем выберите вид диаграммы, который подходит Вам больше всего. Потом нажмите «ОК». Я буду строить с маркерами, но в данном случае можно было бы также сделать гистограмму, или линейчатую диаграмму.

Дальше в Вашем документе появится новая диаграмма, и откроется новый лист Excel с таблицей.

В нее нужно перенести все значения, которые у Вас указаны в таблице в документе Word.

Сначала нужно выбрать правильный диапазон значений в Excel. У меня будет 5 строк (верхняя строка и 4 сотрудника), и 8 столбцов (имена сотрудников и месяцы). Возьмите за правый нижний угол, и выберите нужное Вам количество строк и столбцов.

Дальше перенесите все из таблицы в Ворд в Excel.

Когда будете их менять, обратите внимание, что и сам график изменяется

После того, как все в Excel, будет изменено, закройте это окно.

У меня получился вот такой результат.

Если кликнуть два раза левой кнопкой мыши по вертикальной (0, 10, 20, 30…), горизонтальной (Катя, Маша…) оси, легенде (Январь, Февраль…) или любому из рядов данных (цветные кривые), откроется окно с настройками.

Например, нажмем на кривую со значениями за Апрель, открывается окно «Формат ряда данных». Здесь можно поменять цвет, тип линий и прочее.

Если кликнуть по горизонтальной оси, откроется окно «Формат оси». В нем можете выбрать необходимые параметры.

Если кликнуть правой кнопкой мышки по самому графику, откроется контекстное меню. В нем можно «Изменить данные» – появится лист Excel с созданной таблицей, который мы закрыли, «Изменить тип диаграммы» и другое.

Кликнув по созданному графику, вверху появится вкладка «Работа с диаграммами». В ней Вы увидите еще три дополнительные вкладки: «Конструктор», «Макет» и «Формат». Поклацайте по ним, и посмотрите, как еще можно поменять вид. Например, добавьте название к диаграмме.

После создания, работа с графиком в Ворде ничем не отличается от работы с ним в Excel. Поэтому можете прочесть статью: как сделать график в Excel.

Yotx.ru

Замечательный русскоязычный сервис, осуществляющий построение графиков онлайн по точкам (по значениям) и графиков функций (обычных и параметрических).

Этот сайт обладает интуитивно понятным интерфейсом и легок в использовании. Не требует регистрации, что существенно экономит время пользователя.

Позволяет быстро сохранять готовые графики на компьютере, а также генерирует код для размещения на блоге или сайте.

На Yotx.ru есть учебник и примеры графиков, которые были созданы пользователями.

Возможно, для людей, углубленно изучающих математику или физику, этого сервиса будет мало (например, нельзя построить график в полярных координатах, так как на сервисе нет логарифмической шкалы), но для выполнения самых простых лабораторных работ вполне достаточно.

Преимуществом сервиса является то, что он не заставляет как многие другие программы, искать полученный результат по всей двумерной плоскости.

Размер графика и интервалы по осям координат автоматически генерируются так, чтобы график оказался удобным для просматривания.

Одновременно на одной плоскости есть возможность построить несколько графиков.

Дополнительно на сайте можно использовать калькулятор матриц, с помощью которого легко производить различные действия и преобразования.