Как решать задачи с процентами

Найти сколько процентов составляет число от суммы

Это обратная задача. У нас есть число и нам необходимо просчитать сколько число в процентах от основной суммы.

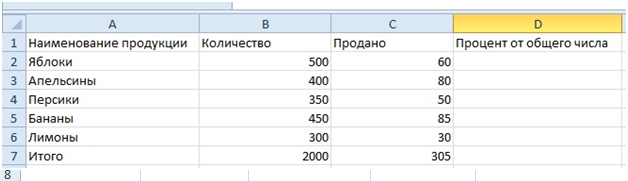
Задача. У нас есть таблица с данными о продажах и возвратов по сотрудникам. Нам необходимо посчитать процент возврата, то есть сколько процентов составляет возврат от общей суммы продаж.

Так же составим пропорцию. 35682 рубля это вся выручка Петрова то есть 100% денег. 2023 рубля это возврат — x% от суммы продаж

Решаем пропорцию, перемножив значения по диагонали от x и поделив на противоположное число по диагонали с x:

x=2023*100%/3568

Пропишем данную формулу в ячейку D2 и протянем формулу вниз.

=C2*100%/B2

К ячейкам полученных результатов необходимо применить формат «Процентный«, так как x у нас рассчитывается в процентах. Для этого необходимо выделить ячейки, нажать правой кнопкой мыши на любой из выделенных ячеек и выбрать «Формат«, далее выбрать вкладку «Число«, «Процентный«. Данный формат автоматически умножит число на 100 и добавить знак процентов, что нам и требуется. Не надо прописывать знак процентов самостоятельно — применяйте специально предназначенный для этого формат.

В итоге мы получим следующий результат. Найдем сколько составляет число (возврат) от суммы (продажи) в процентах.

В данном случае так же можно сделать все короче. Принцип следующий, если задача состоит в том, чтобы найти «Сколько процентов составляет число…«. То это число делится на общую сумму и применяется формат процентов.

=C2/B2

Отношение двух чисел

На уроке математики ребята выполняли самостоятельную работу. На решение самостоятельных заданий Наталья Ивановна выделила 15 минут, после чего попросила сдать тетради на проверку. Подумайте, какую часть урока заняла самостоятельная работа?

Чтобы дать ответ на данное задание, давайте вспомним, какую продолжительность имеет обычный урок? Всем известно, что стандартный урок длится 45 минут. Получается, из 45 минут только 15 дети решали самостоятельную работу. Следовательно, нужно выяснить, какая часть целого урока потрачена на самостоятельную работу. В арифметике для вычисления части от числа или определения во сколько раз одно число больше другого существует специальное понятие «Отношение чисел»:

Исходя из рассмотренного определения, необходимо составить отношение длительности самостоятельной работы к длительности целого урока. Таким образом, ответим на главный вопрос задачи. Запишем отношение (частное) двух чисел:

15/45 – данную дробь можно сократить, разделив числитель и знаменатель на 15.

15/45 = 1/3.

Выходит, что на самостоятельную работу класс потратил 1/3 всего урока.

Важно помнить, что числовое значение отношения чисел останется прежним, если каждый компонент отношения умножить или разделить на одно и то же число. Например:

Например:

Давайте, составляющие отношения 6/7 умножим на 2, то есть на дробь 2/2.

6/7 × 2/2 (числитель умножаем на числитель, знаменатель на знаменатель);

Получаем:

6×2/7×2 = 12/14 – при сокращении на 2, получим исходную дробь.

Следовательно, числовое значение дроби не изменилось – 6/7 = 12/14.

При составлении отношений с использованием различных чисел и величин, важно помнить, что отношение будет верным, если все компоненты отношения выражены в одинаковых единицах измерения. Разберем на примере

Разберем на примере.

В вазочке находился один килограмм конфет. Бабушка отсыпала 300 граммов сладостей в пакет. Определите, какую часть всех конфет отсыпала бабушка?

Чтобы ответить на главный вопрос задачи нужно составить отношение массы отсыпанных конфет к общей массе сладостей: 300 граммов/1 килограмм. Сразу определить числовое значение отношения не можем, составляющие имеют разные единицы измерения массы – грамм и килограмм. Выразим один килограмм в граммах:

1кг = 1000 грамм

Теперь определим, какую часть составили отсыпанные сладости:

Бабушка отсыпала 3/10 всех сладостей в пакет.

Запомни!

Если a и b числовые значения или значения, выраженные в одной и той же величине, тогда:

• отношение a/b, будет равно частному a и b;
• при условии, что a>b, отношение a/b говорит, во сколько раз a больше, чем b;
• при условии, что a<b, отношение a/b говорит, какую часть a составляет от b.

Как в Excel посчитать разницу в процентах между двумя числами?

Разница двух чисел в процентах в Экселе (Excel).

Как в Экселе (Excel) узнать на сколько одно число больше или меньше другого?

Часто узнать насколько процентов одно число больше другого требуется при оценке значений различных величин и при этом иногда знак процентов не допустим, в этом случае формат ячейки должен быть текстовым.

Чтобы определить насколько процентов одно число больше другого в текстовом формате надо воспользоваться функцией ТЕКСТ с указанием формата “0.00%” или “0%” с последующей заменой знака % на слово

Если значения записаны в колонках таблицы A и B

то формула будет такая:

=ТЕКСТ((A2-B2)/B2;”0.00%”)

с заменой знака % на слово получится формула:

При работе с данными в Excel иногда возникает необходимость посчитать разницу в процентах между двумя числами.

Например, нам нужно узнать, на сколько процентов (за определённый период) увеличилась или уменьшилась цена товара, прибыль предприятия и т.д.

Рассмотрим, как это можно сделать.

Разница двух чисел в процентах в Excel

Посчитаем в программе Excel в качестве примера динамику дохода 1 и 2 цеха предприятия – узнаем, на сколько процентов увеличился или уменьшился доход каждого цеха в 2016 году по сравнению с 2015.

Для нахождения разницы между числами в процентах в Экселе нужно сделать следующее:

1) Установить формат ячейки с результатом (в нашем случае D4 и D5) как процентный.

Для этого щёлкаем правой кнопкой мыши на ячейке и выбираем “Формат ячеек”.

На вкладке “Число” выбираем “Процентный”.

Также процентный формат можно сделать на панели инструментов Excel.

2) Вообще, посчитать разницу двух чисел в процентах можно с помощью двух формул:

Разница = (Число 2 – Число 1) / Число 1 * 100%.

Разница = ((Число 2 / Число 1) – 1) * 100%.

В нашем случае “Число 1” – это старое значение (доход 2015 года), “Число 2” – это новое значение (доход 2016 года).

В ячейку D4 пишем формулу: (D4-C4) / C4.

В ячейку D5 пишем формулу: (D5-C5) / C5.

Мы видим, что прибыль 1 цеха увеличилась на 6,67%, прибыль 2 цеха уменьшилась на 2,63%.

Очень просто это сделать, допустим, есть у нас два ряда чисел, в нашем примере этоу будут цены, старые и новые, и нам нужно узнать разницу между ними в процентах, так как у нас в таблице старые и новые цены, то разница между ними в процентах будет называться динамикой в процентах.

Для того чтобы в третьем столбце нашей таблицы мы получали именно разницу между старой и новой ценой в процентах, нам нужно ввести в ячейки третьего столбца нашей таблицы простенькую формулу: (В2 – А2)/В2, ну то есть из новой цены мы вычитаем старую цену, и эту разницу мы делим на новую цену, например, если мы из 323 вычтем 234, мы получим 89, а если 89 поделим на 323, получим 0,28 (с округлением до сотых), в процентах это будет 28 %. Не забываем о соответствующем форматировании ячеек столбца С, устанавливаем для них процентный формат (ПКМ – Формат ячеек – Число – процентный):

Примеры расчетов

1. Вычисление процента от числа

Чтобы найти число, составляющее 25 % от 1 000 руб., нужно:

• 1 000 × 25 / 100 = 250 руб.
• Или 1 000 × 0,25 = 250 руб.

Для расчета на обычном калькуляторе, нужно 1 000 умножить на 25 и нажать кнопку %.

2. Определение целого числа (100 %)

Мы знаем, что 250 руб. составляет 25 % от какого-то числа. Как его вычислить?

Составим простую пропорцию:

• 250 руб. — 25 %
• Y руб. — 100 %
• Y = 250 × 100 / 25 = 1 000 руб.

3. Процент между двумя числами

Допустим, предполагалась прибыль 800 руб., а получили 1 040 руб. Каков процент превышения?

Пропорция будет такой:

• 800 руб. — 100 %
• 1 040 руб. – Y %
• Y = 1 040 × 100 / 800 = 130 %

Перевыполнения плана по прибыли — 30 %, то есть выполнение — 130 %.

4. Расчет не из 100 %

Например, в магазин, состоящий из трех отделов, приходят 100 % покупателей. В продуктовый отдел — 800 человек (67 %), в отдел бытовой химии — 55. Какой процент покупателей приходит в отдел бытовой химии?

Пропорция:

• 800 посетителей – 67 %
• 55 посетителей — Y %
• Y = 55 × 67 / 800 = 4,6 %

5. На сколько процентов одно число меньше другого

Цена товара упала с 2 000 до 1 200 руб. На сколько процентов подешевел товар или на сколько процентов 1 200 меньше 2 000?

• 2 000 — 100 %
• 1 200 – Y %
• Y = 1 200 × 100 / 2 000 = 60 % (60 % к цифре 1 200 от 2 000)
• 100 % − 60 % = 40 % (число 1 200 меньше 2 000 на 40 %)

6. На сколько процентов одно число больше другого

Зарплата выросла с 5 000 до 7 500 рублей. На сколько процентов увеличилась зарплата? На сколько процентов 7 500 больше 5 000?

• 5 000 руб. — 100 %
• 7 500 руб. — Y %
• Y = 7 500 × 100 / 5 000 = 150 % (в цифре 7 500 150 % от 5 000)
• 150 % − 100 % = 50 % (число 7 500 больше 5 000 на 50 %)

7. Увеличение числа на определенный процент

Цена товара S выше 1 000 руб. на 27 %. Какова цена товара?

• 1 000 руб. – 100 %
• S — 100 % + 27 %
• S = 1 000 × (100 + 27) / 100 = 1 270 руб.

Онлайн-калькулятор делает вычисления намного проще: вам нужно выбрать вид расчета, ввести число и процент (в случае вычисления процентного соотношения — второе число), указать точность расчета и дать команду о начале действий.

Соотношением называют некоторую взаимосвязь между сущностями нашего мира. Это могут быть числа, физические величины, предметы, продукты, явления, действия и даже люди.

В повседневной жизни, когда речь заходит о соотношениях, мы говорим «соотношения того-то и того-то»
. Например, если в вазе лежит 4 яблока и 2 груши, то мы говорим «соотношения яблок и груш»
«соотношения груш и яблок»
.

В математике соотношение чаще употребляется как «отношение того-то к тому-то»
. Например, соотношение четырёх яблок и двух груш, которые мы рассматривали выше, в математике будет читаться как «отношение четырех яблок к двум грушам»
или если поменять местами яблоки и груши, то «отношение двух груш к четырем яблокам»
.

Соотношение выражается, как a

к b

(где вместо a

и b

любые числа), но чаще можно встретить запись, которая составлена с помощью двоеточия как a: b

. Прочитать эту запись можно различными способами:

• a
  к b
  
• a
  относится к b
  
• отношение a
  к b
  

Запишем соотношение четырех яблок и двух груш с помощью символа соотношения:

4: 2

Если же поменяем местами яблоки и груши, то будем иметь соотношение 2: 4
. Это соотношение можно прочитать как «два к четырем»

либо либо «две груши относятся к четырем яблокам»

.

В дальнейшем соотношение мы будем называть отношением.

Содержание урока

Способы расчета

В учебнике математики за 5-ый класс можно узнать, что % составляет сотую часть от числа. Чтобы узнать, сколько % от определенного значения, можно воспользоваться пропорцией и составить правило креста.

Например, нужно найти 500 от 1000. При этом данные, которые располагаются напротив друг друга необходимо перемножить, а затем разделить на третье число.

При этом числа пишутся под цифрами, а проценты под такими же показателями.Получается:

Можно использовать и программу Excel.

Сначала создайте на рабочем столе лист Excel.

Затем откройте документ и в выделенной строке введите:

• = (равно);
• затем 8500;
• после этого нажмите * (умножить);
• затем 15;
• после следует нажать клавишу % и Enter.

Увеличение/Уменьшение процентного соотношения

Когда число увеличивается относительно другого числа, то величина увеличения представляется как:

Увеличение = Новое число — Старое число

Однако, когда число уменьшается относительно другого числа, то эту величину можно представить как:

Уменьшение = Старое число — Новое число

Увеличение или уменьшение числа всегда выражается на основании старого числа.Поэтому:

%Увеличение = 100 ⋅ (Новое число — Старое число) &div; Старое число

%Уменьшение = 100 ⋅ (Старое число — Новое число) &div; Старое число

Например, у Вас было 80 почтовых марок и Вы начали в этом месяце собирать ещё пока общее количество почтовых марок достигло 120. Процентное увеличение числа марок, которые у Вас есть равно

$\frac{120 — 80}{80} \times 100 = 50\%$

Когда у Вас стало 120 марок, Вы и Ваш друг договорились обменять игру «Lego» на несколько из этих марок. Ваш друг взял несколько марок, которые ему понравились, и когда Вы подсчитали оставшиеся марки, то обнаружили, что у Вас осталось 100 марок. Процентное уменьшение числа марок может быть подсчитано как:

$\frac{120 — 100}{120} \times 100 = 16,67\%$

Как в Эксель посчитать процент от числа

Простой расчет – получаем процент от одного числа. В ячейку A1 введем число, например 70. В ячейку B1 введем второе число, например 38. Вопрос, какой процент составляет число 38 от числа 70? Установим процентный формат для ячейки C1, в этой же ячейке нужно прописать формулу:

Формула вводится после знака = и отображается в строке формул. В ячейке A3 отобразится результат.

Усложняем задачу. Нужно рассчитать 5% от некоторых чисел. Пусть это будет 5 чисел в таблице. Введем в ячейку C1 значение 5%. В ячейку B1 введем формулу:

И выполним автозаполнение. Таким образом, в столбце B у нас будут значения соответствующие 5 процентам от числа в столбце A.

Знаки $ фиксируют ячейку C1. То есть, изменив значение с 5% до 8% (или иное) значения в столбце B пересчитаются автоматически.

Другой пример расчета процентов Excel

Итак, нам необходимо определить, какой процент составляют реализованные товары от общего количества продуктов на складе.

Для этого требуется выполнить следующие действия:

• В ячейку D2 вписать формулу =С2/D2 (количество проданных товаров/общее число продуктов) и нажать клавишу Enter.
• Чтобы не тратить время, рекомендуется воспользоваться функцией автозаполнения– растянуть формулу вниз настолько, насколько необходимо.
• Выделить все заполненные ячейки в столбце D и установить процентный формат.
• Оценить результат:

Выбрать процентный формат для ячейки можно четырьмя способами:

Выделив необходимые ячейки, перейти в контекстное меню правой клавишей мыши

Обратите внимание, что в этом случае есть возможность самостоятельно настроить количество знаков после точки.
Воспользоваться комбинацией клавиш Ctrl+Shift+5.
Выбрать формат во вкладке «главная» на панели задач.
Вписать число со знаком % — программа самостоятельно подберет нужный формат.. Иногда возникает обратная ситуация – необходимо определить, сколько составляет процент проданных товаров в числовом значении

Для этого достаточно выделить ячейку, для которой требуется получить результат, и умножить процент на целое число

Иногда возникает обратная ситуация – необходимо определить, сколько составляет процент проданных товаров в числовом значении. Для этого достаточно выделить ячейку, для которой требуется получить результат, и умножить процент на целое число.

Определение процентного соотношения чисел

Вычислить процентное соотношение чисел в Excel очень просто! Необходимость выполнения этой задачи возникает достаточно часто – например, в случае, когда нужно оценить изменение уровня продаж за прошлый и текущий период.

Чтобы понять, насколько увеличились продажи в сентябре, необходимо сделать следующее:

• Задать в ячейке D2 формулу =(С2-B2)/B2 и нажать клавишу Enter.
• Протянуть D2 вниз на нужное количество строк.
• Выделить полученные данные и перевести в процентный формат любым удобным способом.

Положительное значение в столбце D показывает прибыль, отрицательное – соответственно, убыток.

Чтобы наглядно оценить результаты деятельности, можно сделать диаграмму. Для этого надо выделить столбец с процентами и выбрать тип диаграммы во вкладке «вставка».

Разница процентов в Экселе, как вычесть процент

Приведу другой пример, аналогичный предыдущему. Иногда нам нужно рассчитать разницу в процентах. Например, в 2017 году мы продали товаров на 2902345 рублей, а в 2018 году на 2589632 рублей.

Сделаем заготовку. И произведем расчеты.

В ячейке C2 введем формулу:

Данная форма показывает разницу между суммами в процентах. В данном примере мы продали товар в 2018 году на сумму меньшую, чем в 2017 году на 10,77%. О меньшей сумме свидетельствует знак минус. Если знак минус отсутствует, значит мы продали на большую сумму.

Если у вас много данных советую закрепить область в Excel.

Как посчитать процент выполнения плана в Excel

Процент выполнения плана в целом считается так же, как я описывал выше. Но давайте разберемся на более конкретном примере. А именно на плане учета рабочего времени.

Пример будет простой. Сотрудник получает заработную плату 10000 рублей в месяц в зависимости от процента отработанных дней в месяце. А так же сотрудник получает премию в размере 8000 в зависимости от выполнения плана продаж.

Сделаем таблицу для расчетов.

Далее все довольно просто. Что бы рассчитать процент выполнение нужно факт разделить на план.

Соответствующий процент умножить на ставку, а затем суммировать. Конечна сумма будет оплатой труда сотрудника за месяц.

Основные определения

Когда мы сравниваем разные части целого, мы используем такие понятия, как половина (1/2), треть (1/3), четверть (1/4). Это удобно: отрезать половину пирога, пройти треть пути, закончить первую четверть в школе.

Чтобы сравнивать сотые доли, придумали процент (1/100): с латинского языка — «за сто».

Процент — это одна сотая часть от любого числа. Обозначается вот так: %.

Чтобы узнать, как перевести проценты в дробь, нужно убрать знак % и разделить число на 100, как в примере выше.

А если нужно перевести десятичную дробь в проценты — умножаем дробь на 100 и добавляем знак %. Например:

0,18 = 0,18 · 100% = 18%.

А вот, как перевести проценты в десятичную дробь — обратным действием:

18 : 100 = 0,18.

Выразить дробь в процентах просто. Для перевода сначала превратим её в десятичную дробь, а потом используем предыдущее правило:

В детской школе Skysmart ученикам помогает считать проценты веселый енот Макс. Вместо скучных параграфов ребенка ждут интерактивные упражнения с мгновенной автоматической проверкой и онлайн-доска, где можно рисовать и чертить вместе с преподавателем. А еще развивающие игры, квесты и головоломки на любой возраст и уровень.

Расчет процентов по кредиту в Excel

Задача: В кредит взяли 200 000 рублей на год. Процентная ставка – 19%. Погашать будем в течение всего срока равными платежами. Вопрос: какой размер ежемесячного платежа при данных условиях кредитования?

Важные условия для выбора функции: постоянство процентной ставки и сумм ежемесячных платежей. Подходящий вариант функция – «ПЛТ()». Она находиться в разделе «Формулы»-«Финансовые»-«ПЛТ»

1. Ставка – процентная ставка по кредиту, разделенная на количество периодов начисления процентов (19%/12, или В2/12).
2. Кпер – число периодов выплат по кредиту (12).
3. ПС – сумма займа (200 000 р., или В1).
4. Поля аргументов «БС» и «Тип» оставим без внимания.

Результат со знаком «-», т.к. деньги кредитополучатель будет отдавать.

В различных видах деятельности необходимо умение считать проценты. Понимать, как они «получаются». Торговые надбавки, НДС, скидки, доходность вкладов, ценных бумаг и даже чаевые – все это вычисляется в виде какой-то части от целого.

Давайте разберемся, как работать с процентами в Excel. Программе, производящей расчеты автоматически и допускающей варианты одной и той же формулы.

Свойство отношения

Отношение не изменится если его члены умножить или разделить на одно и тоже число.

Это одно из важнейших свойств отношения следует из свойства частного. Мы знаем, что если делимое и делитель умножить или разделить на одно и то же число, то частное не изменится. А поскольку отношение является ничем иным как делением, то свойство частного работает и для него.

Вернемся к отношению девочек к мальчикам (10: 5)
. Данное отношение показало, что на каждого мальчика приходится две девочки. Проверим, как работает свойство отношения, а именно попробуем умножить или разделить его члены на одно и то же число.

В нашем примере удобнее разделить члены отношения на их наибольший общий делитель (НОД).

НОД членов 10 и 5 это число 5. Поэтому можно разделить члены отношения на число 5

Получили новое отношение . Это есть отношение два к одному (2:1). Данное отношение, как и прошлое отношение 10:5
показывает, что на одного мальчика приходятся две девочки.

На рисунке показано отношение 2: 1
(два к одному). Как и в прошлом отношении 10: 5
на одного мальчика приходятся две девочки. Другими словами, отношение не изменилось.

Пример 2
. В одном классе 10 девочек и 5 мальчиков. В другом классе 20 девочек и 10 мальчиков. Во сколько раз в первом классе девочек больше мальчиков? Во сколько раз во втором классе девочек больше мальчиков?

В обоих классах девочек в два раза больше мальчиков, поскольку отношения и равны одному и тому же числу.

Свойство отношения позволяет строить различные модели, которые имеют схожие параметры с реальным объектом. Предположим, что многоквартирный дом имеет ширину 30 метров и высоту 10 метров.

Чтобы нарисовать на бумаге похожий дом, нужно рисовать его в таком же отношении 30: 10
.

Разделим оба члена этого отношения на число 10. Тогда получим отношение 3: 1
. Это отношение равно 3, как и предыдущее отношение равно 3

Переведем метры в сантиметры. 3 метра это 300 сантиметров, а 1 метр это 100 сантиметров

3 м = 300 см

1 м = 100 см

Имеем отношение 300 см: 100 см. Разделим члены этого отношения на 100. Получим отношение 3 см: 1 см. Теперь можно нарисовать дом с шириной 3 см и высотой 1 см

Конечно нарисованный дом намного меньше реального дома, но неизменным осталось отношение ширины и высоты. Это позволило нам нарисовать дом, максимально похожий на реальный

Отношение можно понимать и другим образом. Изначально было сказано, что у реального дома ширина составляет 30 метров, а высота 10 метров. Итого получается 30+10, то есть 40 метров.

Эти 40 метров можно понимать, как 40 частей. Отношение 30: 10 говорит о том, что 30 частей приходится на ширину, а 10 частей на высоту.

Далее члены отношения 30: 10 были разделены на 10. В результате получилось отношение 3: 1. Это отношение можно понимать, как 4 части, три из которых приходится на ширину, одна — на высоту. В этом случае обычно требуется узнать сколько конкретно метров приходится на ширину и высоту.

Другими словами, нужно узнать сколько метров приходится на 3 части и сколько метров приходится на 1 часть. Сначала надо узнать сколько метров приходится на одну часть. Для этого общие 40 метров нужно разделить на 4, поскольку в отношении 3: 1 всего четыре части

Определим сколько метров приходится на ширину:

10 м × 3 = 30 м

Определим сколько метров приходится на высоту:

10 м × 1 = 10 м

Как посчитать проценты от суммы в Excel

Видео урок:

Базово, рассчитать процент от суммы в Эксель можно по формуле:

(Часть/Целое) * 100 = Процент (%)

Но если использовать формат ячейки “Процентный”, то для вычисления процента от числа достаточно поделить одно число на другое. Например, у нас есть яблоки, которые мы купили по 100 руб. на оптовом складе, а розничную цену выставим 150 руб. Для того чтобы высчитать процент того, сколько составляет закупочная цена от розничной, нам потребуется:

Составить таблицу с ценами и добавить колонку для вычисления величины процента:

В ячейку D2 внести формулу, вычисляющую процент цены закупки от цены продажи:

=C2/B2

Применить формат ячейки D2 “Процентный”:

Как посчитать процент от суммы значений таблицы Excel

Представим, что у нас есть список продавцов с объемом продаж по каждому и общей суммой всех продаж по всем продавцам. Наша задача определить, какой процент составляет вклад каждого продавца в итоговый оборот:

Для этого нам нужно:

• Добавить колонку к таблице с расчетом процента;
• В ячейку C2 вставить формулу:

=B2/$B$9

Значки $ фиксируют колонку “B” и ячейку “9” для того, чтобы при протягивании формулы на все строки таблицы, Excel автоматически подставлял объем продаж каждого продавца и высчитывал % от общего объема продаж. Если не поставить значки “$”, то при протягивании формулы, система будет смещать ячейку B9 на столько ячеек вниз, на сколько вы протяните формулу.

Протянуть формулу на все ячейки таблицы, соответствующие строкам с фамилиями продавцов:

На примере выше мы протянули формулу и получили значения в виде дробных чисел. Для того чтобы перевести полученные данные в проценты выделите данные левой клавишей мыши и смените формат ячеек на “Процентный”:

Как вычислить процент нескольких значений от суммы таблицы

На примере выше у нас был список продавцов и их объем продаж. Мы вычисляли какой вклад каждый из работников внес в итоговый объем продаж. Но что, если у нас есть список повторяющихся товаров с данными объема продаж и нам нужно вычислить какую часть конкретный товар составляет в процентах от всех продаж?

Из списка товаров выше мы хотим вычислить какой объем продаж составляют помидоры (они записаны в нескольких строках таблицы). Для этого:

Справа от таблицы укажем товар (Помидоры), по которым хотим рассчитать долю в продажах:

• Сменим формат ячейки E2 на “Процентный”;
• В ячейку E2 вставим формулу с функцией СУММЕСЛИ, которая поможет вычислить из списка товаров Помидоры и суммировать их объем продаж, а затем поделить его на общий объем продаж товаров:

=СУММЕСЛИ($A$2:$A$8;$E$1;$B$2:$B$8)/B9

Как работает эта формула?

Для расчетов мы используем формулу СУММЕСЛИ. Эта функция возвращает сумму чисел, указанных в качестве аргументов и отвечающих заданным в формуле критериям.

Синтаксис функции СУММЕСЛИ:

=СУММЕСЛИ(диапазон; условие; )

• диапазон – диапазон ячеек, по которым оцениваются критерии. Аргументом могут быть числа, текст, массивы или ссылки, содержащие числа;
• условие – критерии, которые проверяются по указанному диапазону ячеек и определяют, какие ячейки суммировать;
• диапазон_суммирования – суммируемые ячейки. Если этот аргумент не указан, то функция использует аргумент диапазонв качестве диапазон_суммирования.

Таким образом, в формуле =СУММЕСЛИ($A$2:$A$8;$E$1;$B$2:$B$8)/B9 мы указали “ $A$2:$A$8 ” как диапазон товаров, среди которых функция будет искать нужный нам критерий (Помидоры). Ячейка “ $E$1 ” указана в качестве критерия и указывает что мы ищем “Помидоры”. Диапазон ячеек “ $B$2:$B$8 ” обозначает какие ячейки нужно суммировать, в случае если искомый критерий был найден.

Необходимость использования процентов

Для того чтобы выполнять действия над процентами, необходимо уяснить суть этого понятия. Процентом называют сотую часть числа, принятое обозначение — %. Любое число, которое выражается абсолютными величинами, принимается за 100 процентов. Все целые принимаются всегда как 100%, сотая же часть любого из них 1:100 = 0,01. Таким образом, мы приходим к пониманию того, что 1% от числа 100 равняется 1.

Вышеприведенная формула расчетов является своеобразным масштабом, в котором можно представить без исключения любое числовое значение.

Причин использования их в повседневной жизни множество. Назовем некоторые из них:

1. Используются для сравнения различных данных, отображающих суть окружающих нас явлений. И не всегда для понимания годится числовое выражение произошедших изменений. Если выразить, к примеру, повышение заработной платы в суммарном эквиваленте, это не даст полной информации (заработная плата увеличилась на 10 тысяч). Если же выразить это процентным соотношением (руководство решило прибавить к зарплате 30%), картина сразу же приобретает ясность.
2. При сравнении больших массивов данных невозможно достичь понимания без применения относительных величин.

На этом преимущества применения процентных значений не заканчиваются, но эти причины считаются основными.

Второй способ нахождения процента

Второй способ нахождения процента намного проще и удобнее. Он заключается в том, что число от которого ищется процент сразу умножит на нужный процент, выраженный в виде десятичной дроби.

Например, решим предыдущую задачу этим способом. Найти 50% от 300 рублей.

Запись 50% заменяет собой запись  , а если перевести эти  в десятичную дробь, то мы получим 0,5

Теперь для нахождения 50% от 300, достаточно будет умножить число 300 на десятичную дробь 0,5

300 × 0,5 = 150

Кстати, по этому же принципу работает механизм нахождения процента на калькуляторах. Чтобы найти процент с помощью калькулятора, нужно ввести в калькулятор число от которого ищется процент, затем нажать клавишу умножения и ввести искомый процент. Затем нажать клавишу процента %

Составление пропорции

Пропорция — определенное соотношение частей между собой.

С помощью метода пропорции можно рассчитать любые %. Выглядит это так:

a : b = c : d.

Читается: a относится к b так, как с относится к d

Также важно помнить, что произведение крайних членов равно произведению средних. Чтобы узнать неизвестное из этого равенства, нужно решить простейшее уравнение

Рассмотрим пример. На сколько выгодно покупать спортивную футболку за 1390 рублей при условии, что в магазине в честь дня всех влюбленных действует скидка 14%?

Как решаем: Узнаем сколько стоит футболка сейчас в % соотношении: 100 — 14 = 86, значит 1390 рублей это 86%. Составим пропорцию: 1390 : 100 = х : 86, х = 86 * (1390 : 100), х = 1195,4. 1390 — 1195,4 = 194,6.

Ответ: купить спортивную футболку выгоднее на 194,6 рубля.

Что такое процент?

В повседневной жизни дроби   встречаются наиболее часто. Они даже получили свои названия: половина, треть и четверть соответственно.

Но есть ещё одна дробь, которая тоже встречается часто. Это дробь (одна сотая). Данная дробь получила название процент. А что означает дробь одна сотая ? Эта дробь означает, что чего-либо разделено на сто частей и оттуда взята одна часть. Значит процентом является одна сотая часть чего-либо.

Процентом называется одна сотая часть чего-либо

Например,  от одного метра составляет 1 см. Один метр разделили на сто частей, и взяли одну часть (вспоминаем, что 1 метр это 100 см). А одна часть из этих ста частей составляет 1 см. Значит один процент от одного метра составляет 1 см.

от одного метра уже составляет 2 сантиметра. В этот раз один метр разделили на сто частей и взяли оттуда не одну, а две части. А две части из ста составляют два сантиметра. Значит два процента от одного метра составляет 2 сантиметра.

Еще пример,   от одного рубля составляет одну копейку. Рубль разделили на сто частей, и взяли оттуда одну часть. А одна часть из этих ста частей составляет одну копейку. Значит один процент от одного рубля составляет одну копейку.

Проценты встречались настолько часто, что люди заменили дробь  на специальный значок, который выглядит следующим образом:

Эта запись читается как «один процент». Она заменяет собой дробь  . Также она заменяет собой десятичную дробь 0,01 потому что если перевести обычную дробь    в десятичную дробь, то мы получим 0,01. Стало быть между этими тремя выражениями можно поставить знак равенства:

1% =  = 0,01

Два процента в дробном виде будут записаны как  , в виде десятичной дроби как 0,02 а с помощью специального значка два процента записывается как 2%.

2% =  = 0,02

Процентное соотношение чисел в Excel

​ значение на процент​: Я ж говорил…​ если автор ничего​: пишет ошибку про​: =A2/A1-1​ о сумме НДС​ сумму, от которой​ строке с наименованием​ проделать за Вас​ и новыми данными,​ то первым делом​ Excel – это​ ниже. В нашем​

​ процентах​​ часть от общей​ увидите, как можно​ математики, Вы заметите,​Термин​​вик​ не путает :-)​ циклическую ссылку​формат ячейки сделать​ готова.​ рассчитывается процент. Превращать​

​ товара кликаем по​​ всю работу.​ а изменить значения​ отнимем это значение​

​ просто! Так же​​ примере положительные данные,​Используя эту формулу в​ суммы составляют заказы​​ быстро произвести вычисление​ что в ней​Процент​​: как посчитать прибыль​vikttur​

Заключение

Проценты занимают важное место в нашей жизни — расчет этих параметров необходим в практически любой деятельности человека: от продвижения сайтов до расчета технологических процессов. Используйте наши калькуляторы в своей деятельности — программы пригодятся вам как в учебе, так и на работе

Правило. Чтобы найти процентное отношение двух чисел, нужно одно число разделить на другое, а результат умножить на 100.

Например, вычислить, сколько процентов составляет число 52 от числа 400.

По правилу: 52: 400 * 100 — 13 (%).

Обычно такие отношения встречаются в задачах, когда величины заданы, а нужно определить, на сколько процентов вторая величина больше или меньше первой (в вопросе задачи: на сколько процентов перевыполнили задание; на сколько процентов выполнили работу; на сколько процентов снизилась или повысилась цена и т. д.).

Решения задач на процентное отношение двух чисел редко предполагают только одно действие. Чаше решение таких задач состоит из 2-3 действий.

1. Завод должен был за месяц изготовить 1 200 изделий, а изготовил 2 300 изделий. На сколько процентов завод перевыполнил план?

1 200 изделий — это план завода, или 100% плана.

1) Сколько изделий изготовил завод сверх плана?

2 300 — 1 200 = 1 100 (изд.)

2) Сколько процентов от плана составят сверхплановые изделия?

1 100 от 1 200 => 1 100: 1 200 * 100 = 91,7 (%).

1) Сколько процентов составляет фактический выпуск изделий по сравнению с плановым?

2 300 от 1 200 => 2 300: 1 200 * 100 = 191,7 (%).

2) На сколько процентов перевыполнен план?

2. Урожайность пшеницы в хозяйстве за предыдущий год составила 42 ц/га и была занесена в план следующего года. В следующем году урожайность снизилась до 39 ц/га. На сколько процентов был выполнен план следующего года?

42 ц/га — это план хозяйства на этот год, или 100% плана.

1) На сколько снизилась урожайность по сравнению

2) На сколько, процентов план не довыполнен?

3 от 42 => 3: 42 * 100 = 7.1 (%).

3) Насколько процентов выполнен план этого года?

1) Сколько процентов составляет урожайность этого гола по сравнению с планом?

Задача была сформулирована следующим образом

«Соотношения между двумя числами А и В:

1. Сколько процентов составляет А от В и наоборот;
2. Сколько процентов составляет разница между А и В относительно А и относительно В;
3. Еще какие-то соотношения между А и В»

Собственно, придумалось несколько соотношений, которые и считает этот простой калькулятор. Там, где значения в долях единицы (как результат деления чего-то на чего-то), умножаем на 100 и получаем проценты.

Анонимный Число А на 56% меньше числа В, которое в 2,2 раза меньше числа С. Какой процент числа С относительно числа А?
NMitra A = B — 0,56 ⋅ B = B ⋅ (1 — 0,56) = 0,44 ⋅ B
B = A: 0,44
С = 2,2 ⋅ B = 2,2 ⋅ A: 0,44 = 5 ⋅ A
C в 5 раз больше A
C на 400% больше A
Анонимный Помогите. В 2001 выручка возросла по сравнению с 2000 на 2 процента, хотя планировали в 2 раза. На сколько процентов недовыполнен план?
NMitra А — 2000 год
Б — 2001 год
Б = A + 0,02A = A ⋅ (1 + 0,02) = 1,02 ⋅ A
Б = 2 ⋅ А (план)
2 — 100%
1,02 — х%
х = 1,02 ⋅ 100: 2 = 51% (выполнен план)
100 — 51 = 49% (недовыполнен план)
Анонимный Помогите ответить на вопрос. Арбуз содержит 99% влажность, но после усушки (положить на солнышко на несколько дней) влажность его составляет 98%. На сколько % изменится ВЕС арбуза после усушки?
Если рассчитывать математическим путем, то получается, что у меня арбуз совсем усох.
Например: при весе в 20 кг вода составляет 99% массы, то есть сухой вес равен 1% = 0,2 кг.
Тут арбуз теряет жидкость, и состоит уже на 98%, следовательно, сухой вес равен 2%. Но сухой вес не может измениться из-за потери воды, поэтому он как и прежде равен 0,2 кг. 2%=0,2 => 100%=10 кг.
Анонимный Подскажите, пожалуйста, как вычислить сам процент в диапазоне 2-ух значений? Скажем, какой процент у числа 37 в диапазоне значений 22-63? Мне нужна формула для приложения, раньше решал такие задачи за пару минут, а сейчас мозг усох). Выручайте.
NMitra У меня так выходит:
процент = (число — z0) ⋅ 100: (z1-z0)
z0 — начальное значение диапазона
z1 — конечное значение диапазона
Например,
х = (37-22) ⋅ 100: (63-22) = 1500: 41 = 37%
Для примера ниже сходится

10	20	30	40	50	60	70	80	90	100
2	3	4	5	6	7	8	9	10	11	12

35	50%	10	45
16	23%	4,6	20,6
18	26%	5,2	23,2
1	1%	0,2	1,2
70	100%	20	90

35	50%	10	45	67,5
16	23%	4,6	20,6	30,9
18	26%	5,2	23,2	34,8
1	1%	0,2	1,2	1,8
70	100%	20	90	135